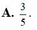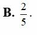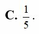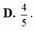Đặt ngẫu nhiên 4 bạn An, Xuân, Lan và Thanh ngồi vào 4 ghế A, B, C và D. Tính XS để An được ngồi vào ghế A?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 1 2019
Chọn A
Số phần tử của không gian mẫu: n ( Ω ) = 5!
Gọi A:”Hai bạn An và Bình không ngồi cạnh nhau”
Thì A ¯ :”Hai bạn An và Bình ngồi cạnh nhau”
Xếp An và Bình ngồi cạnh nhau coi như 1 phần tử
- Xếp 1 phần tử (An+Bình) và 3 bạn còn lại theo các thứ tự khác nhau có: 4! Cách
- Xếp 2 học sinh An và Bình ngồi cạnh nhau có 2! cách
Suy ra 
CM
9 tháng 2 2017
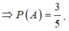
Chọn đáp án A
Phương pháp
Sử dụng nguyên lí vách ngăn.
Cách giải
n(Ω)=5!=120
Xếp Cường, Dũng, Đông vào 3 ghế bất kì có 3! cách, khi đó tạo ra 4 khoảng trống. Xếp An và Bình vào hai trong 4 khoảng trống đó có 4.3 = 12 cách.
Gọi A là biến cố: “An và Bình không ngồi cạnh nhau
CM
5 tháng 7 2017
a) Không gian mẫu là kết quả của việc sắp xếp bốn bạn vào 4 vị trí
⇒n( Ω) = 4! = 24.
Gọi A: “ Sắp xếp nam, nữ ngồi đối diện nhau”.
=> Biến cố đối A− : “ Nam ngồi đối diện nam, nữ ngồi đối diện nữ”
+ Ta tính P(A−):
Có 4 chỗ để cho bạn nữ thứ nhất chọn.
Có 1 cách chọn cho bạn nữ thứ hai ( đối diện với bạn nữ thứ nhất).
Sau khi hai bạn nữ đã được chọn ( ngồi đối diện nhau) thì còn lại 2 chỗ đối diện nhau để xếp 2 bạn nam và có 2! Cách xếp 2 bạn nam này.
Theo quy tắc nhân có: 4.1.2! = 8 cách xếp chỗ sao cho nam ngồi đối diện nam, nữ ngồi đối diện nữ
Do đó,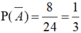 
Suy ra, xác suất biến cố A là:
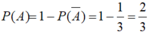
b) Theo phần trên xác suất để nữ ngồi đối diện nhau ( khi đó hai nam cũng ngồi đối diện nhau) là:
CM
24 tháng 12 2019
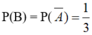
Chọn D
Số phần tử của không gian mẫu: 
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
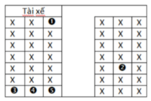
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
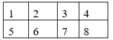
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
