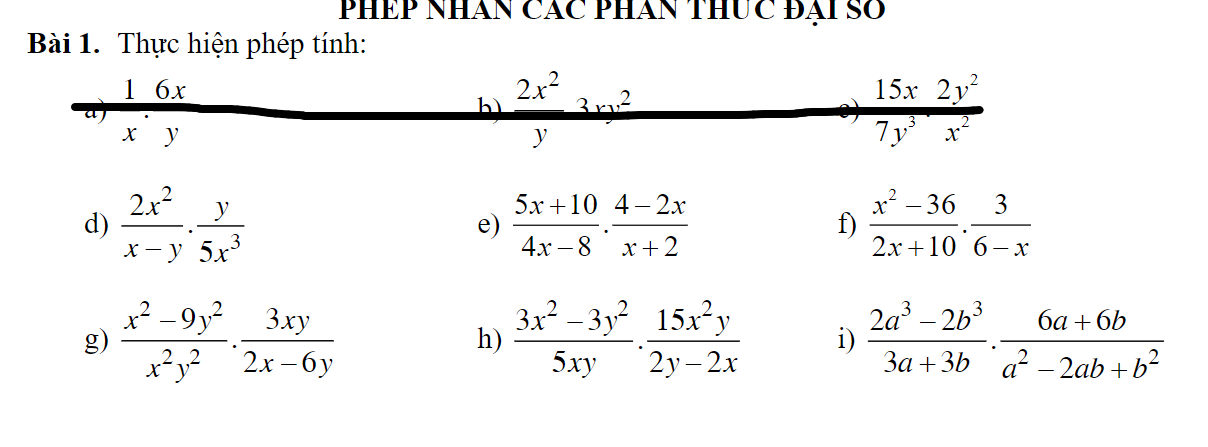dạ câu 18 den 30 e giải không dc ạ giúp e với, e cảm ơn nhiều ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LT
0
Những câu hỏi liên quan
MA
2
15 tháng 11 2021
\(d,=\dfrac{3y}{5x\left(x-y\right)}\\ e,=\dfrac{5x\left(x+2\right)\left(2-x\right)}{4\left(x-2\right)\left(x+2\right)}=\dfrac{-5x}{4}\\ f,=\dfrac{3\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)\left(6-x\right)}=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\\ g,=\dfrac{3xy\left(x-3y\right)\left(x+3y\right)}{2x^2y^2\left(x-3y\right)}=\dfrac{3\left(x+3y\right)}{2xy}\\ h,=\dfrac{45x^2y\left(x-y\right)\left(x+y\right)}{10xy\left(y-x\right)}=\dfrac{-9x\left(x+y\right)}{2}\\ i,=\dfrac{12\left(a-b\right)\left(a+b\right)\left(a^2+ab+b^2\right)}{3\left(a+b\right)\left(a-b\right)^2}=\dfrac{4\left(a^2+ab+b^2\right)}{a-b}\)
15 tháng 11 2021
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)
LT
0
TT
0
23 tháng 2 2022
a: BC=35cm
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
hay BD/21=CD/28
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó: BD=15cm; CD=20cm
b: Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/21=20/35=4/7
=>DE=12cm
Xét ΔABC có DE//AB
nên DE/AB=CE/CA
=>12/21=CE/28
=>CE/28=4/7
=>CE=16(cm)
25 tháng 2 2022
a) -Xét △AMB có: MD là tia phân giác của \(\widehat{AMB}\) (gt)
\(\Rightarrow\)\(\dfrac{AM}{BM}=\dfrac{AD}{BD}\) (định lí đường phân giác trong tam giác)
-Xét △AMC có: ME là tia phân giác của \(\widehat{AMC}\) (gt)
\(\Rightarrow\)\(\dfrac{AM}{CM}=\dfrac{AE}{CE}\) (định lí đường phân giác trong tam giác)
Mà \(BM=CM\) (M là trung điểm BC).
\(\Rightarrow\)\(\dfrac{AM}{BM}=\dfrac{AE}{CE}\)
Mà \(\dfrac{AM}{BM}=\dfrac{AD}{BD}\left(cmt\right)\) nên \(\dfrac{AD}{BD}=\dfrac{AE}{CE}\).
-Xét △ABC có: \(\dfrac{AD}{BD}=\dfrac{AE}{CE}\) (cmt)
\(\Rightarrow\) DE//BC (định lí Ta-let đảo).
b) -Xét △ABM có: DG//BM.
\(\Rightarrow\dfrac{DG}{BM}=\dfrac{AG}{AM}\) (hệ quả định lí Ta-let).
--Xét △ACM có: EG//CM.
\(\Rightarrow\dfrac{EG}{CM}=\dfrac{AG}{AM}\)(hệ quả định lí Ta-let).
Mà \(\dfrac{DG}{BM}=\dfrac{AG}{AM}\) (cmt) ; \(BM=CM\) (M là trung điểm BC)
\(\Rightarrow\) \(DG=EG\) nên G là trung điểm DE.
*Giả sử G là trung điểm AM.
-Ta có: \(\widehat{AMB};\widehat{AMC}\) là 2 góc kề bù.
Mà MB, MC lần lượt là tia phân giác của \(\widehat{AMB},\widehat{AMC}\) (gt)
\(\Rightarrow\widehat{DME}=90^0\) (định lí về góc được tạo bởi hai tia phân giác của 2 góc kề bù).
-Xét tứ giác AEMD có:
G là trung điểm của AM (gt)
G là trung điểm của DE (cmt)
\(\Rightarrow\) AEMD là hình bình hành mà \(\widehat{DME}=90^0\) (cmt)
\(\Rightarrow\) AEMD là hình chữ nhật nên \(\widehat{BAC}=90^0\).
-Vậy △ABC vuông tại A thì G là trung điểm AM.
c) -Ta có: \(AB^2+AC^2=12^2+16^2=400\left(cm\right)\); \(BC^2=400\left(cm\right)\)
\(\Rightarrow AB^2+AC^2=BC^2\)
-Xét △ABC có: \(AB^2+AC^2=BC^2\) (cmt)
\(\Rightarrow\)△ABC vuông tại A (định lí Py-ta-go đảo).
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.12.16=96\left(cm^2\right)\)
-Ta có: \(\dfrac{S_{ABC}}{S_{ACM}}=\dfrac{BC}{CM}\) (△ABM, △ABC có cùng đỉnh A và B,M,C thẳng hàng).
Mà \(BC=2CM\) (M là trung điểm BC).
\(\Rightarrow\dfrac{S_{ABC}}{S_{ACM}}=\dfrac{2CM}{CM}=2\)
\(\Rightarrow S_{ACM}=\dfrac{S_{ABC}}{2}=\dfrac{96}{2}=48\left(cm^2\right)\)
-Xét △ABC có: AN là tia phân giác của \(\widehat{BAC}\) (gt)
\(\Rightarrow\)\(\dfrac{AB}{AC}=\dfrac{BN}{CN}\) (định lí đường phân giác trong tam giác).
Mà \(\dfrac{BN}{CN}=\dfrac{S_{ABN}}{S_{ACN}}\)(△ABN, △ACN có cùng đỉnh A và B,N,C thẳng hàng).
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{S_{ABN}}{S_{ACN}}\)
\(\Rightarrow\dfrac{S_{ABN}}{S_{ACN}}=\dfrac{12}{16}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{S_{ABN}}{S_{ACN}}+1=\dfrac{3}{4}+1\)
\(\Rightarrow\dfrac{S_{ABC}}{S_{ACN}}=\dfrac{7}{4}\)
\(\Rightarrow S_{ACN}=\dfrac{4}{7}.S_{ABC}=\dfrac{4}{7}.96=\dfrac{384}{7}\left(cm^2\right)\)
-Vì \(AB< AC\left(12cm< 16cm\right)\) nên \(BN< CN\)
\(\Rightarrow S_{ANM}=S_{ACN}-S_{ACM}=\dfrac{384}{7}-48=\dfrac{48}{7}\left(cm^2\right)\)
MA
1
30 tháng 9 2021
a) Đặt \(a=x^2+x\)
Đa thức trở thành: \(a^2-14a+24=\left(a^2-14a+49\right)-25=\left(a-7\right)^2-25=\left(a-7-5\right)\left(a-7+5\right)=\left(a-12\right)\left(a-2\right)\)
Thay a:
\(\left(a-12\right)\left(a-2\right)=\left(x^2+x-12\right)\left(x^2+x-2\right)\)
b) Đặt \(a=x^2+x\)
Đa thức trở thành:
\(\left(x^2+x\right)^2+4x^2+4x-12=\left(x^2+x\right)^2+4\left(x^2+x\right)-12=a^2+4a-12=\left(a^2+4x+4\right)-16=\left(a+2\right)^2-16=\left(a+2-4\right)\left(a+2+4\right)=\left(a-2\right)\left(a+6\right)\)
Thay a:
\(\left(a-2\right)\left(a+6\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)\)
JP
1
6 tháng 3 2022
a.Áp dụng định lý pitago vào tam giác vuông PKQ, ta có:
\(QK^2=PQ^2+PK^2\)
\(\Rightarrow QK=\sqrt{6^2+8^2}=\sqrt{100}=10cm\)
Áp dụng t/c đường phân giác góc P, ta có:
\(\dfrac{PQ}{PK}=\dfrac{AP}{AK}\)
\(\Leftrightarrow\dfrac{6}{8}=\dfrac{AP}{AK}\) \(\Leftrightarrow\dfrac{3}{4}=\dfrac{AP}{AK}\) \(\Leftrightarrow\dfrac{AK}{4}=\dfrac{AP}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{AK}{4}=\dfrac{AP}{3}=\dfrac{AK+AP}{4+3}=\dfrac{QK}{7}=\dfrac{10}{7}\)
\(\Rightarrow AK=\dfrac{10}{7}.4=\dfrac{40}{7}cm\)
\(\Rightarrow AP=\dfrac{10}{7}.3=\dfrac{30}{7}cm\)
b. Xét tam giác PBQ và tam giác PQK, có:
\(\widehat{PBQ}=\widehat{QPK}=90^0\)
\(\widehat{Q}:chung\)
Vậy tam giác PBQ đồng dạng tam giác PQK ( g.g )
\(\Rightarrow\dfrac{PB}{PK}=\dfrac{PQ}{QK}\)
\(\Leftrightarrow\dfrac{PB}{8}=\dfrac{6}{10}\) \(\Leftrightarrow\dfrac{PB}{8}=\dfrac{3}{5}\)
\(\Leftrightarrow5PB=24\) \(\Leftrightarrow PB=\dfrac{24}{5}cm\)
c. Xét tam giác PBQ và tam giác PBK, có:
\(\widehat{PBQ}=\widehat{PBK}=90^0\)
\(\widehat{PQB}=\widehat{BPK}\) ( cùng phụ với \(\widehat{A}\) )
Vậy tam giác PBQ đồng dạng tam giác PBK ( g.g )
\(\Rightarrow\dfrac{PB}{BK}=\dfrac{QB}{PB}\)
\(\Leftrightarrow PB^2=BK.QB\)
