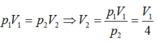cho một khí lí tưởng đơn nguyên tử có thể tích 5 lít ở áp suất 1 atm và nhiệt điị 300K (A) khi thực hiện quá trình biến đổi đẳng tính đến áp suất 3 atm (B) sau đó giẳn đẳng nhiệt về áp suất 1 atm (C) cuối cùng khi được làm lạnh đẳng áp đến thể tích ban đầu (A) tính a) nhiệt độ tại B và C b) nhiệt hệ nhận và công khối khí thực hiện trong chu trình trên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
17 tháng 2 2021
Tóm tắt đề bài như sau:
\(\left\{{}\begin{matrix}V=10\left(l\right)\\p=2\left(atm\right)\\T=87+273=360\left(K\right)\end{matrix}\right.\underrightarrow{Đẳngáp}\left\{{}\begin{matrix}V_1=?\\p_1=2\left(atm\right)\\T_1=\dfrac{T}{2}=180\left(K\right)\end{matrix}\right.\) \(\underrightarrow{Đẳngnhiet}\left\{{}\begin{matrix}V_2=?\\p_2=0,5\left(atm\right)\\T_2=180\left(K\right)\end{matrix}\right.\)
Phương trình trạng thái khí lí tưởng ( Claperon Mendeleep ): \(\dfrac{pV}{T}=const\)
Đẳng áp: \(\dfrac{V}{T}=\dfrac{V_1}{T_1}\Leftrightarrow V_1=\dfrac{10.180}{360}=5\left(l\right)\)
Đẳng nhiệt: \(p_1V_1=p_2V_2\Rightarrow V_2=\dfrac{p_1V_1}{p_2}=\dfrac{2.5}{0,5}=20\left(l\right)\)
Vậy thể tích sau cùng của khối khí trên là V2=20(l)
ID
9 tháng 5 2022
Áp dụng định lí Bô lơ - Mariốt:
\(p_1\times V_1=p_2\times V_2\rightarrow3\times2=p_2\times5\)
\(\rightarrow p_2=1.2atm\)
2
15 tháng 5 2022
Áp dụng định luật Bôi lơ - Ma ri ốt có:
`p_1.V_1=p_2.V_2`
`=>4.V_2=9.3`
`=>V_2=6,75(l)`
16 tháng 5 2022
Ta có
\(\dfrac{p_1}{V_1}=\dfrac{p_2}{V_2}\\ \Rightarrow V_1=\dfrac{p_1V_2}{p_2}=1,\left(3\right)l\)
