Hai dây dẫn bằng nhôm có chiều dài tiết diện và điện trở tương ứng là l1 S1 R1 và l2 S2 R2 biết là l1 = 4 l2 và S1 = S2s . Hãy lập luận nào về mối quan hệ giữa các điện trở r1 và R2 của dây dẫn này
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C. Chiều dài lớn gấp 4 thì điện trở lớn gấp 4 lần, tiết diện lớn gấp 2 thì điện trở nhỏ hơn 2 lần, Vậy R 1 = 2 R 2

Chiều dài lớn gấp 4 lần thì điện trở lớn gấp 4 lần, tiết diện lớn gấp 2 lần thì điện trở nhỏ hơn 2 lần => R1 = 2.R2
→ Đáp án C

Dây thứ nhất có: R 1 , l 1 , S 1
Dây thứ hai có: R 2 , l 2 , S 2
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l 3 = l 2 nhưng lại có tiết diện S 3 = S 1
Như vậy dây 1 và dây 3 có cùng vật liệu và tiết diện nhưng khác chiều dài.
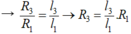
Lại có dây 2 và dây 3 có cùng vật liệu, cùng chiều dài, khác tiết diện.
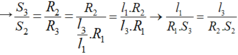
Thay
S
3
=
S
1
,
l
3
=
l
2
→ 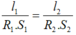 → Chọn D
→ Chọn D

\(5,6W=5,6\Omega;16,8W=16,8\Omega\)
\(\dfrac{R_1}{R_2}=\dfrac{\dfrac{l_1}{S_1}}{\dfrac{l_2}{S_2}}=\dfrac{l_1.S_2}{S_1.l_2}\Rightarrow l_2=\dfrac{l_1.S_2}{S_1}:\dfrac{R_1}{R_2}=\dfrac{200.1.10^{-6}}{2.10^{-6}}:\dfrac{5,6}{16,8}=300\left(m\right)\)

+ Dự đoán: Nếu tiết diện tăng gấp hai hoặc ba lần thì điện trở của dây giảm hai hoặc ba lần: R2 = R/2 và R3 = R/3
+ Các dây dẫn có cùng chiều dài và làm từ cùng một vật liệu, nếu tiết diện của dây tăng bao nhiêu lẩn thì điện trở của nó giảm bấy nhiêu lần.
Từ đó suy ra điện trở của các dây dẫn có cùng chiều dài và làm từ cùng một vật liệu thì tỉ lệ nghịch vớí tiết diện của nó.
Hệ thức liên hệ: 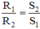

Áp dụng công thức: 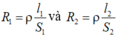 (hai dây này cùng làm bằng một loại vật liệu)
(hai dây này cùng làm bằng một loại vật liệu)
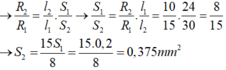

Dây thứ nhất có: l 1 = 200m, S 1 = 1 m m 2 , R 1 = 5,6Ω
Dây thứ hai có: l 2 = ? m, S 2 = 2 m m 2 , R 2 = 16,8 Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l 3 = l 1 = 200m nhưng lại có tiết diện S 3 = S 2 = 2 m m 2 .
Như vậy dây 1 và dây 3 có cùng vật liệu và chiều dài, khác tiết diện
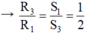
→ R 3 = R 1 /2 = 2,8Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng tiết diện, khác chiều dài
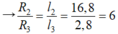
→ l 2 = 6 l 1 = 6.200 = 1200m

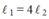
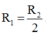
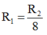
S1=2S2 à bạn?
R1 = \(\rho_{Nhôm}\dfrac{l_1}{S_1}\)
R2 = \(\rho_{Nhôm}\dfrac{l_2}{S_2}\)
\(\dfrac{R_1}{R_2}=\dfrac{\rho_{Nhôm}\dfrac{l_1}{S_1}}{\rho_{Nhôm}\dfrac{l_2}{S_2}}=\dfrac{l_1}{S_1}:\dfrac{l_2}{S_2}=\dfrac{l_1}{S_1}\cdot\dfrac{S_2}{l_2}=\dfrac{1}{4\cdot2}=\dfrac{1}{8}\)
cho mik hoi p nhom la j z