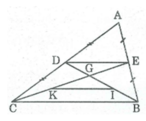
Cho tam giác ABC , các đường trung tuyến BD, CE cắt nhau tại G. Gọi I , K lần lượt là trung điểm của GB, GC. Chứng minh rằng
a) IK là đường trung bình của tam giác GBC
b) IK=ED và IK//ED
c ) IE = KD và IE //KD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 8 2020
Mình không biết vẽ hình trên đây nên bạn thông cảm nhé
a,Xét tam giác GBC có: GI=BI(I là trung điểm của GB)
GK=CK(K là trung điểm của GC)
=>IK là đường trung bình của tam giác GBC
b, Vì IK là đường trung bình của tam giác GBC
=> \(\hept{\begin{cases}IK=\frac{1}{2}BC\\IKsongsongBC\end{cases}}\)(1)
Vì BD là đường trung tuyến kẻ từ B của tam giác ABC =>AD=CD
Vì CE là đường trung tuyến kẻ từ C của tam giác ABC =>AE=BE
Xét tam giác ABC có: AD=CD
AE=BE
=>DE là đường trung bình của tam giác ABC
=>\(\hept{\begin{cases}DE=\frac{1}{2}BC\\DEsongsongBC\end{cases}}\)(2)
Từ (1) và (2)=>\(\hept{\begin{cases}IK=ED\\IKsongsongED\end{cases}}\)
24 tháng 9 2021
Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
I là trung điểm của GB
K là trung điểm của GC
Do đó: IK là đường trung bình của ΔGBC
Suy ra: IK//BC và \(IK=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra IK//ED và IK=ED
20 tháng 8 2020
a) Xét tam giác GBC có:
I là trung điểm GB, K là trung điểm GC => IK là đường trung bình tam giác GBC(đpcm)
b) Xét tam giác ABC có:
BD là trung tuyến => D là trung điểm AC
CE là trung tuyến =>E là trung điểm AB
==>> ED là đường trung bình tam giác ABC => ED= 1/2 BC (1) và ED//BC(2)
Ta có: IK là đường trung bình tam giác GBC => IK= 1/2 BC (3) và IK//BC (4)
Từ (1) và (3) => ED=IK (đpcm)
Từ (2) và (4) => ED//IK (đpcm)
K cho mk nha!!!!!
8 tháng 9 2017
(Bạn tự vẽ hình nhé!)
a, Xét tam giác ABC, có:
E là trung điểm AB (gt)
D là trung điểm AC (gt)
=> ED là đường trung bình tam giác ABC
=> ED // BC, ED = \(\dfrac{1}{2}\) BC (t/c) (1)
Xét tam giác GBC, có:
I là trung điểm GB (gt)
K là trung điểm GC (gt)
=> IK là đường trung bình tam giác GBC
=> IK // BC, IK = \(\dfrac{1}{2}\) BC (t/c) (2)
Từ (1) và (2) => IK = ED và IK // ED
b, Vì IK // ED (cmt)
=> EDKI là hình thang
Mà IK = ED (cmt) và hai cạnh này chính là hai đáy của hình thang EDKI
=> IE = KD và IE // KD
KV
15 tháng 9 2017
Cho tam giác ABC, M là trung điểm của BC. Trên cạnh AB lấy D và E sao cho AD= DE= EB. Gọi I là trung điểm của AM và CD. Chứng minh I là trung điểm của AM
CM
9 tháng 2 2018
* Trong ∆ ABC, ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của ∆ ABC
⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)
* Trong ∆ GBC, ta có:
I là trung điểm của BG (gt)
K là trúng điểm của CG (gt)
Nên IK là đường trung bình của ∆ GBC
⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)
Từ (l) và (2) suy ra: IK // DE, IK = DE.
26 tháng 7 2017
a. Xét \(\Delta ABC\)
Ta có \(\hept{\begin{cases}AE=EB\\AD=DC\end{cases}\Rightarrow DE}\)là đường trung bình của tam giác ABC
\(\Rightarrow\)DE song song BC và \(DE=\frac{1}{2}BC\left(1\right)\)
Xét \(\Delta BGC\)có \(\hept{\begin{cases}BI=IG\\CK=KG\end{cases}\Rightarrow IK}\)là đường trung bình của tam giác BGC
\(\Rightarrow\)IK song song BC và \(IK=\frac{1}{2}BC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow DE\)song song \(IK\)và \(DE=IK\)
b. Theo tính chất của trọng tâm ta có
\(GF=\frac{1}{3}AF\);\(AG=\frac{2}{3}AF\left(3\right)\)
Xét \(\Delta ABG\)có IE là đường trung bình suy ra \(IE=\frac{1}{2}AG\left(4\right)\)
Từ (3) và (4) \(\Rightarrow IE=\frac{1}{2}AG=\frac{1}{2}.\frac{2}{3}AF=\frac{1}{3}AF=GF\)
Vậy \(IE=GF\)
25 tháng 10 2022
Cho tam giác ABC các đường trung tuyến BD và CE cắt nhau tại G gọi I và K theo thứ tự là trung điểm của GB GC
a tứ giác BIKC lF hình gì ? Vì sao?
b tú giác EDKI là hình gì ? Vì sao?
a) xét tg BGC có : BI=IG (gt) ; GK=KC (gt) => IK// BC => IK là đtb tg BGC
chỉ có thể giải v thui thông cảm nha