Cho hình thang ABCD có hai đáy là AB và CD . Gọi E , F , K lần lượt là trung điểm của các cạnh AD , BC ,BD .
a ) Chứng minh EK//AB , KF//AB và E , F , K thẳng hàng
b) Gọi I là giao điểm EF và AC . Chứng minh : IA = IC
c ) Chứng minh : IE = KF và KE = IF
d ) Cho biết AB = 6cm , CD = 10cm . Tính IK.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
10 tháng 9 2018
.png)
a) Xét tam giác ABD có E và K lần lượt là trung điểm của AD và DB nên EK là đường trung bình tam giác ABD.
Vậy thì EK // AB
Hoàn toàn tương tự ta có ngay KF // DC, hay KF // AB.
Ta thấy, từ một điểm K có hai đoạn thẳng EK và KF cùng song song với AB. Theo tiên đề Oclit ta có E, K, F thẳng hàng.
b) Xét tam giác ABC có F là trung điểm BC, IF // AB nên IF là đường trung bình tam giác ABC.
Vậy thì AI = IC.
c) Xét tam giác ADC có E, I lần lượt là trung điểm của AD và AC nên EI là đường trung bình tam giác ADC.
Vậy thì \(EI=\frac{DC}{2}\)
Tương tự \(KF=\frac{DC}{2}\)
Vậy nên EI = KF.
Từ đó ta có: EI - KI = KF - KI hay EK = IF.
d) Ta có KF = DC/2 = 10 : 2 = 5 (cm)
IF = AB/2 = 6 : 2 = 3 (cm)
Vậy thì KI = KF - IF = 2 (cm)
5 tháng 11 2017
a) Hình thang ABCD có:
E là trung điểm của AD (1)
F là trung điểm của BC
=> EF là đường trung bình của hình thang ABCD
nên EF// CD
=> EK // CD (2)
Từ (1)(2) => KA = KC
b) * Xét tam giác ACD có:
EA =ED (gt)
KA = KC (cmt)
=> EK là đường trung bình của tam giác ACD
=>EK = 1/2 CD
=>CD = 6 x 2
CD= 12 cm
* Tương tự chứng minh KF là đường trung bình của tam giác ABC
=> KF =1/2 AB
=>AB = 2 x 2
AB = 4 cm
31 tháng 1 2022
- Hình vẽ:
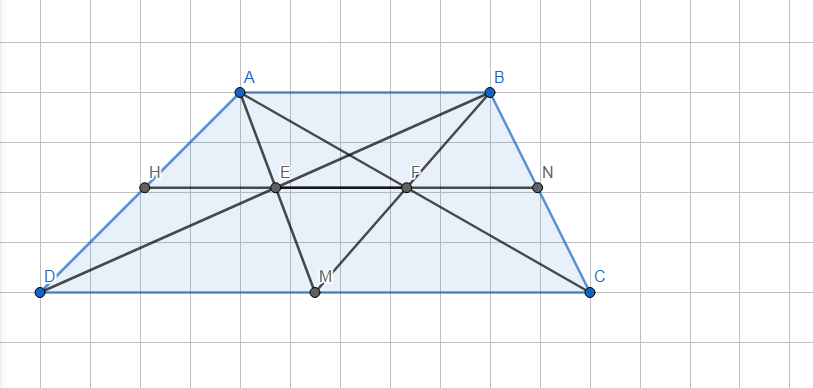
a) - Xét △EDM có:
AB//DM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) (định lí Ta-let) (1).
- Xét △FCM có:
AB//CM (ABCD là hình thang có 2 đáy là AB và CD).
=>\(\dfrac{BF}{MF}=\dfrac{AB}{CM}\) (định lí Ta-let) (2).
- Từ (1) và (2) và \(CM=DM\) (M là trung điểm BC) suy ra:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\).
- Xét △ABM có:
\(\dfrac{AE}{EM}=\dfrac{BF}{MF}\) (cmt)
=>\(EF\)//\(AB\) (định lí Ta-let đảo)nên\(EF\)//\(AB\)//\(CD\)
b) -Xét △ADM có:
HE//DM (cmt).
=>\(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (định lí Ta-let). (3)
- Xét △ACM có:
EF//CM (cmt)
=>\(\dfrac{EF}{CM}=\dfrac{AE}{AM}\) (định lí Ta-let) (4)
- Từ (3) và (4) và \(DM=CM\) (M là trung điểm BC) suy ra: \(HE=EF\)
-Xét △BDM có:
EF//DM (cmt).
=>\(\dfrac{EF}{DM}=\dfrac{BF}{BM}\)(định lí Ta-let). (5)
- Xét △BCM có:
NF//CM (cmt)
=>\(\dfrac{NF}{CM}=\dfrac{BF}{BM}\) (định lí Ta-let) (6)
- Từ (5) và (6) và \(CM=DM\) (M là trung điểm BC) suy ra: \(NF=EF\)
Mà \(HE=EF\) nên \(HE=EF=NF=\dfrac{1}{3}HN\).
c) -Ta có: \(\dfrac{HE}{DM}=\dfrac{AE}{AM}\) (cmt)
=>\(\dfrac{DM}{HE}=\dfrac{AM}{AE}\).
=>\(\dfrac{DM}{HE}-1=\dfrac{EM}{AE}\) (7)
- Ta có: \(\dfrac{AE}{EM}=\dfrac{AB}{DM}\) nên \(\dfrac{EM}{AE}=\dfrac{DM}{AB}\). (8)
- Từ (7) và (8) suy ra:
\(\dfrac{DM}{HE}-1=\dfrac{DM}{AB}\)
=>\(\dfrac{DM}{HE}=\dfrac{DM}{AB}+1=\dfrac{DM+AB}{AB}\)
=>\(HE=\dfrac{AB.DM}{AB+DM}=\dfrac{7,5.\left(12.\dfrac{1}{2}\right)}{7,5+\left(12.\dfrac{1}{2}\right)}=\dfrac{10}{3}\)
=>\(HN=3HE=3.\dfrac{10}{3}=10\) (cm).
