Giúp mình với ạ, mình cảm ơn nhiều ạ! ❤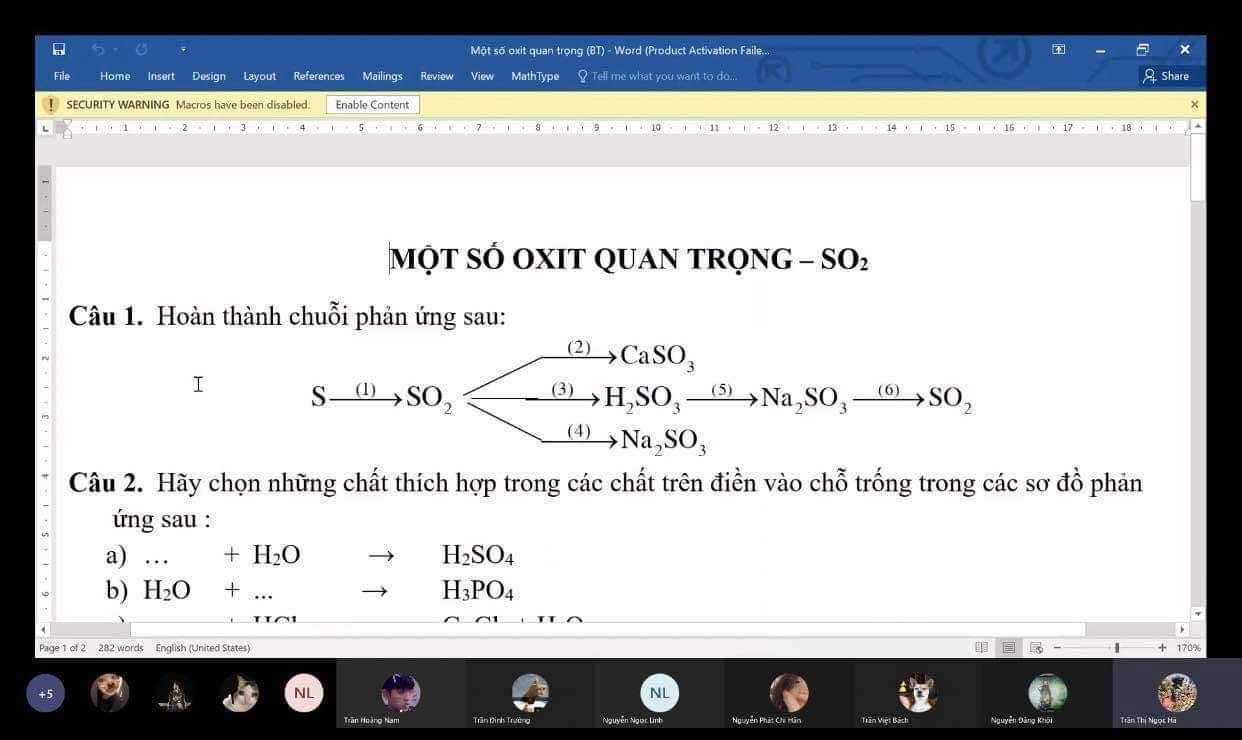
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




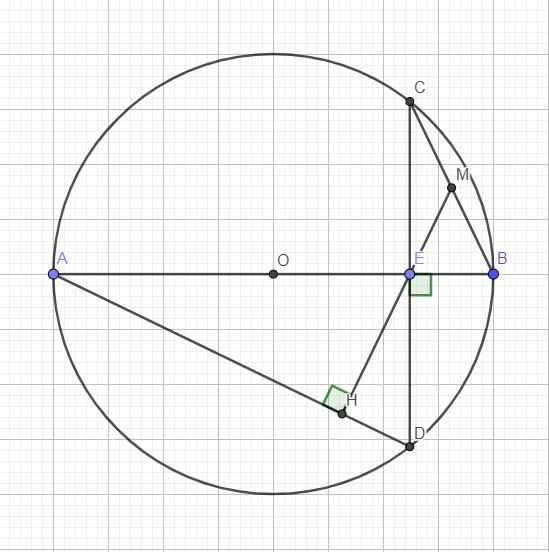
Tứ giác ACBD nội tiếp \(\Rightarrow\widehat{ADC}=\widehat{ABC}\) (cùng chắn AC) (1)
Lại có \(\widehat{ADC}+\widehat{DEH}=90^0\) (tam giác DEH vuông tại H theo gt) (2)
Gọi M là trung điểm BC, nối EM
Trong tam giác vuông BCE, EM là trung tuyến ứng với cạnh huyền
\(\Rightarrow EM=\dfrac{1}{2}BC=BM\Rightarrow\Delta BEM\) cân tại M
\(\Rightarrow\widehat{ABC}=\widehat{MEB}\) (3)
\(\left(1\right);\left(2\right);\left(3\right)\Rightarrow\widehat{DEH}+\widehat{MEB}=90^0\)
\(\Rightarrow\widehat{DEH}+\widehat{MEB}+\widehat{DEB}=90^0+90^0=180^0\)
\(\Rightarrow M;E;H\) thẳng hàng hay HE đi qua trung điểm M của BC

a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Hiệu điện thế giữa hai đầu đoạn mạch :
\(U=I.R_{tđ}=2.24=48\left(V\right)\)
⇒ \(U=U_1=U_2=48\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện chạy qua mỗi điện trở :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{48}{60}=0,8\left(A\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{48}{40}=1,2\left(A\right)\)
Chúc bạn học tốt

b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)

1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

1 They have carried out the project since the government....
2 Mr Han hasn't taken part in the meeting of the ..... for 2 years
3 She has not eaten lobster before
4 This is the first time I have read such a lovely story
5 It is the first time I have met such a famous actor

\(y'=3mx^2-4mx-\left(m+1\right)\)
- Với \(m=0\Rightarrow y'=-1< 0\) hàm nghịch biến trên R (thỏa)
- Với \(m\ne0\) hàm nghịch biến trên R khi:
\(\left\{{}\begin{matrix}3m< 0\\\Delta'=4m^2+3m\left(m+1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\7m^2+3m\le0\\\end{matrix}\right.\)
\(\Leftrightarrow-\dfrac{3}{7}\le m< 0\)
Vậy \(-\dfrac{3}{7}\le m\le0\Rightarrow m=0\)
S có 1 phần tử



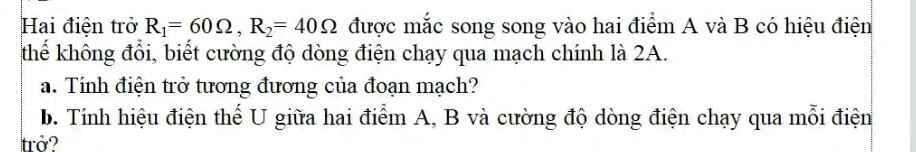
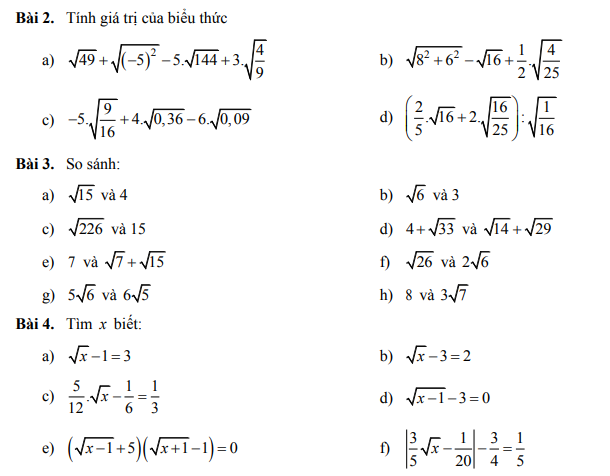 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy

