Tìm số tự nhiên n sao cho A=n4-2n3+3n2-2n là số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
4 tháng 11 2019
Điều kiện xác định của phân thức: n ≠ 2
Ta có:
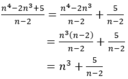
Vậy để N nguyên thì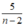 
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì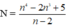 
có giá trị là số nguyên
DY
2
DY
0
TN
1
AH
Akai Haruma
Giáo viên
15 tháng 12 2022
Lời giải:
Đặt $n+31=a^2$ với $a$ tự nhiên. Khi đó: $2n+5=2(a^2-31)+5=2a^2-57$
Như vậy, ta cần tìm $a$ sao cho $2a^2-57$ là số chính phương.
Ta có 1 tính chất quen thuộc: Số chính phương lẻ chia 8 dư $1$ (bạn có thể xét 1 scp $x^2$ và xét các TH $x=4k+...$ để cm)
$\Rightarrow 2a^2-57\equiv 1\pmod 8$
$\Rightarrow 2a^2\equiv 58\pmod 8$
$\Rightarrow a^2\equiv 29\equiv 5\pmod 8$
(điều này vô lý do scp chia 8 dư 0,1 hoặc 4)
Vậy không tồn tại số tự nhiên $a$, tức là không tồn tại số $n$ cần tìm.
KN
1
7 tháng 5 2023
đặt 2n + 34 = a^2
34 = a^2-n^2
34=(a-n)(a+n)
a-n thuộc ước của 34 là { 1; 2; 17; 34} và a-n . Ta có bảng sau ( mik ko bt vẽ)
=> a-n 1 2
a+n 34 17
Mà tổng và hiệu 2 số nguyên cùng tính chẵn lẻ
Vậy ....
7 tháng 5 2023
Ta cóS = 14 +24 +34 +···+1004 không là số chính phương.
=> S= (1004+14).100:2=50 900 ko là SCP
TT
1
N
30 tháng 7 2016
\(a=n^2\left(n^4-n^2+2n+2\right)\)
A=\(n^2\left(n+1\right)\left(n^3-n^2+2\right)\)
A=\(n^2\left(n+1\right)\left(n^3+1-n^2+1\right)\)
A=\(n^2\left(n+1\right)^2\left(n^2-2n+2\right)\)
A=\(n^2\left(n+1\right)^2\left(n-1\right)+n^2\left(n+1\right)^2\)
nhận thấy n^2 -2n+2=\(\left(n-1\right)^2+1>\left(n-1\right)^2\)(1) (vì n>1)
vì n>1 => 2n>2
=>2n-2>0
=>\(n^2-\left(2n-2\right)< n^2\)
hay \(n^2-2n+2< n^2\)(2)
từ (1) và (2) =>\(\left(n-1\right)^2< n^2-2n+2< n^2\)
=>\(n^2-2n+2\)không là số chính phương
=> A= \(n^2\left(n+1\right)^2\left(n^2-2n+2\right)\) không là số chính phương
mình làm tắt chỗ nào không hiểu hỏi mình trả lời cho
Nếu n=0,suy ra A=0(thỏa mãn)
Nếu n=1 suy rs A=0(thỏa mãn)
Nếu n>1,ta có
A=n.(n^3-2.n^2+3n-2)
A=n.[n.(n^2-2n+3)-2]
A=n.[n.(n-1)^2+2.(n-1)]
A=n.(n-1).[n.(n-1)+2]
Ta thấy:[n.(n-1)]^2<A<[n.(n-1)+1]^2 (tự chứng minh)
Suy ra A không phải là số chính phương với n>1
Vậy n={0;1}
nhớ chọn câu trả lời của mình nhe