Cho tam giác DEF có: \(12\widehat{D}=10\widehat{E}=15\widehat{F}\)
a, So sánh các cạnh của tam giác DEF
b, Phân giác của góc E cắt DF tại M. So sánh DM và FM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
9 tháng 4 2018
a/ Ta có \(12\widehat{D}=15\widehat{F}\)
=> \(4\widehat{D}=5\widehat{F}\)
=> \(\widehat{D}=\frac{5}{4}\widehat{F}\)
=> \(\widehat{D}>\widehat{F}\)(1)
và \(10\widehat{E}=15\widehat{F}\)
=> \(2\widehat{E}=3\widehat{F}\)
=> \(\widehat{E}=\frac{3}{2}\widehat{F}\)
=> \(\widehat{E}>\widehat{F}\)(2)
Từ (1) và (2) => \(\widehat{D}>\widehat{E}>\widehat{F}\)
=> EF > DF > DE (quan hệ giữa góc và cạnh đối diện trong tam giác)
DT
10 tháng 5 2022
a) Có DE < DF( 5cm < 12cm)
->góc F< góc E
b) áp dụng đl pytago:
EF^2=DE^2+DF^2=5^2+12^2=169
= > EF=13 (cm)
tam giác DEF có DM là trung tuyến(M là trung điểm của EF) ứng với cạnh huyền
=> DM=EM=MF=EF/2=13/2=6,5cm
24 tháng 2 2022
a: \(\widehat{E}=35^0\)
Xét ΔDEF có \(\widehat{E}< \widehat{F}< \widehat{D}\)
nên FD<DE<EF
b: Xét ΔEDH vuông tại D và ΔEKH vuông tại K có
EH chung
\(\widehat{DEH}=\widehat{KEH}\)
Do đó: ΔEDH=ΔEKH
Suy ra: HD=HK
hay ΔHDK cân tại H
25 tháng 2 2022
a: ˆE=350E^=350
Xét ΔDEF có ˆE<ˆF<ˆDE^<F^<D^
nên FD<DE<EF
b: Xét ΔEDH vuông tại D và ΔEKH vuông tại K có
EH chung
ˆDEH=ˆKEHDEH^=KEH^
Do đó: ΔEDH=ΔEKH
Suy ra: HD=HK
TP
Thảo Phương
CTVVIP
28 tháng 8 2017
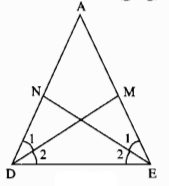
Tam giác ADE có: \(\widehat{\text{D}}=\widehat{E}\)(gt)
\(\widehat{\text{D1}}=\widehat{D2}=\dfrac{1}{2}\widehat{D}\)(Vì DM là tia phân giác)
\(\widehat{\text{E1}}=\widehat{E2}=\dfrac{1}{2}\widehat{E}\)(Vì EN là tia phân giác)
Suy ra:\(\widehat{\text{D1}}=\widehat{D2}=\)\(\widehat{\text{E1}}=\widehat{E2}\)
Xét ∆DNE = ∆EMD, ta có:
\(\widehat{NDE}\widehat{=MED}\)((gt)
DE cạnh chung
\(\widehat{\text{D1}}=\widehat{E2}=\)(chứng minh trên)
Suy ra: ∆DNE = ∆EMD (g.c.g)
Vậy DE = EM (2 cạnh tương ứng).
a: Đặt \(\widehat{D}=a;\widehat{E}=b;\widehat{F}=c\)
Theo đề, ta có: 12a=10b=15c
=>a/5=b/6=c/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{4}=\dfrac{a+b+c}{5+6+4}=\dfrac{180}{15}=12\)
Do đó:a=60; b=72; c=48
Xét ΔDEF có \(\widehat{F}< \widehat{D}< \widehat{E}\)
nên DE<FE<FD
b: Xét ΔDEF có EM là phân giác
nên DM/DE=MF/EF
mà DE<EF
nên DM<MF