a) chứng minh a song song với b
b) chứng minh c vuông góc với b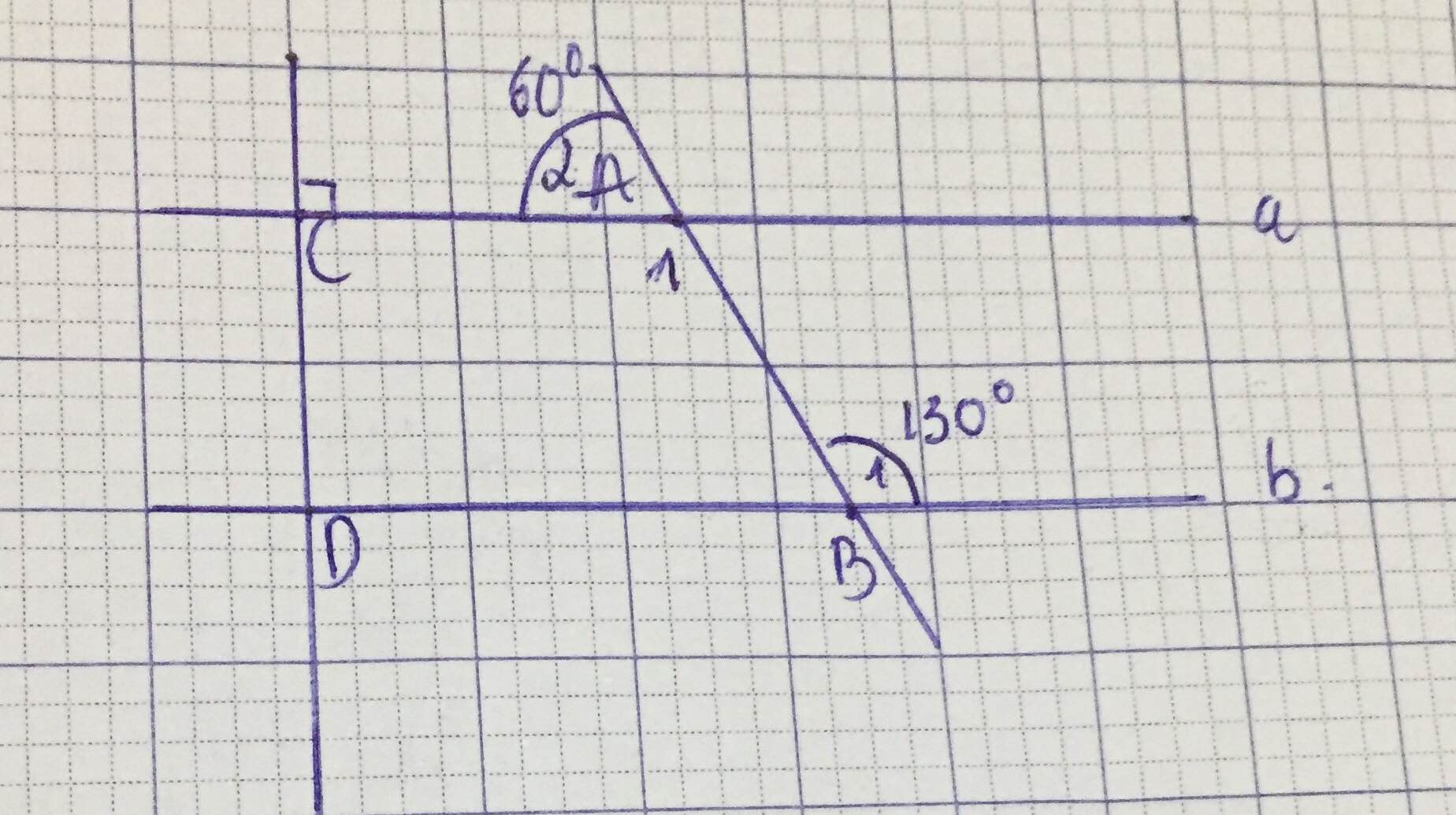
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PP
1
Những câu hỏi liên quan
TN
1
J
4
18 tháng 10 2016
Ta có: a vuông góc c tại A \(\Rightarrow\widehat{A}=90^o\)
Và b vuông góc c tại B \(\Rightarrow\widehat{B}=90^o\)
Mà: \(\widehat{A}=\widehat{B}\) lại đồng vị.
=> a//b
Q
21 tháng 11 2017
a) Ta có \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o ( định lý tổng 3 góc của 1 tam giác )
90o+50o+\(\widehat{C}\) = 180o
140o+\(\widehat{C}\) = 180o
\(\widehat{C}\) = 180o-140o
\(\widehat{C}\) = 40o
b) Vì KH//AC có góc đồng vị tạo thành
Có \(\widehat{BKH}\) đồng vị với \(\widehat{BAC}\)
=> \(\widehat{BKH}\)=\(\widehat{BAC}\)=90o
=> HK vuông góc với AB
c) Ta có góc C = 40o (câu a)
Ta lại có : \(\widehat{HBK}+\widehat{BKH}+\widehat{BHK}=180^o\) (định lý tổng 3 góc của 1 tam giác)
50o+90o+\(\widehat{BHK}\) = 180o
\(\widehat{BHK}\) = 180o-(50o+90o)
=> \(\widehat{BHK}\) = 40o
Vậy góc BHK = góc C ( 40o=40o )
+ AH _|_ BC => \(\widehat{AHB}\) = 90o
Ta có \(\widehat{AHB}+\widehat{B}+\widehat{BAH}\) = 180o (định lý tổng 3 góc của 1 tam giác)
90o+50o+\(\widehat{AHB}\) = 180o
\(\widehat{AHB}\) = 180o-(90o+50o)
=> \(\widehat{AHB}\) = 40o
Vậy \(\widehat{KHB}=\)\(\widehat{AHB}\) (40o=40o)
\(a,\) Muốn chứng minh \(a//b\) thì bạn phải sửa \(\widehat{B_1}=120\) nha
Ta có \(\widehat{A_1}+\widehat{A_2}=180\left(kề.bù\right)\Rightarrow\widehat{A_1}=180-\widehat{A_2}=120\)
Mà \(\widehat{B_1}=120\Rightarrow\widehat{A_1}=\widehat{B_1}\left(=120\right)\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow a//b\)
\(b,\left\{{}\begin{matrix}a\perp c\left(GT\right)\\a//b\left(cmt\right)\end{matrix}\right.\Rightarrow b\perp c\)