Mọi người giúp mình bài này với ạ
K
Khách
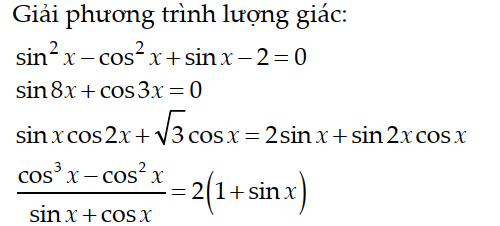
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Mọi người giúp mình bài này với ạ 🙏🙏🙏
13 tháng 8 2021
a) Ta có :
\(x - y = 5\)
\(\frac{x}{2}=\frac{y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{x}{2}=\frac{y}{3}=\frac{x-y}{2-3}=\frac{5}{-1}=-5\)
\(\Rightarrow\hept{\begin{cases}x=-5 . 2 = -10\\y=-5.3=-15\end{cases}}\)
13 tháng 8 2021
b) Ta có :
\(x - y = 9\)
\(\frac{x}{-2}=\frac{y}{-5}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{x}{-2}=\frac{y}{-5}=\frac{x-y}{-2-\left(-5\right)}=\frac{9}{3}=3\)
\(\Rightarrow\hept{\begin{cases}x=3. \left(-2 \right)= -6\\y=3 . \left(-5\right) = -15\end{cases}}\)
23 tháng 8 2021
a)TXĐ:\(D=R\)
b)\(f\left(\dfrac{2}{3}\right)=\left(\dfrac{2}{3}\right)^2+\dfrac{2}{3}-2=-\dfrac{8}{9}\)
\(f\left(3\right)=3-2.3=-3\)
TA
0
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
a.
Đường tròn có tâm \(\left\{{}\begin{matrix}x_I=2m\\y_I=-m-3\end{matrix}\right.\)
\(\Rightarrow x_I+2y_I=2m+2\left(-m-3\right)=-6\)
\(\Leftrightarrow x_I+2y_I+6=0\)
Hay quỹ tích tâm I của đường tròn là đường thẳng có pt: \(x+2y+6=0\)
b.
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}AH=\dfrac{1}{2}AB=3\\IH\perp AB\end{matrix}\right.\) \(\Rightarrow IH=d\left(I;d\right)\)
\(R=IA=\sqrt{\left(2m\right)^2+\left(-m-3\right)^2-\left(5m^2-6m-16\right)}=5\)
\(\Rightarrow IH=\sqrt{IA^2-AH^2}=4\)
\(d\left(I;d\right)=\dfrac{\left|3.2m-4\left(-m-3\right)+12\right|}{\sqrt{3^2+\left(-4\right)^2}}=4\)
\(\Leftrightarrow\left|10m+24\right|=20\Rightarrow\left[{}\begin{matrix}m=-\dfrac{2}{5}\\m=-\dfrac{22}{5}\end{matrix}\right.\)
PT
1
PT
9 tháng 11 2021
bạn giải thích giúp mình bước 1 mấy bước sau mình sẽ tham khảo thêm cảm ơn nhiều 🙏
1 tháng 9 2021
\(\dfrac{1}{\sqrt{\dfrac{5}{7}}+\sqrt{\dfrac{5}{13}}+1}+\dfrac{1}{\sqrt{\dfrac{7}{13}}+\sqrt{\dfrac{7}{5}}+1}+\dfrac{1}{\sqrt{1\dfrac{6}{7}}+\sqrt{2\dfrac{3}{5}}+1}\\ =\dfrac{1}{\dfrac{\sqrt{5}}{\sqrt{7}}+\dfrac{\sqrt{5}}{\sqrt{13}}+\dfrac{\sqrt{5}}{\sqrt{5}}}+\dfrac{1}{\dfrac{\sqrt{7}}{\sqrt{13}}+\dfrac{\sqrt{7}}{\sqrt{5}}+\dfrac{\sqrt{7}}{\sqrt{7}}}+\dfrac{1}{\dfrac{\sqrt{13}}{\sqrt{7}}+\dfrac{\sqrt{13}}{\sqrt{5}}+\dfrac{\sqrt{13}}{\sqrt{13}}}\\ =\left(\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}\right)\cdot\dfrac{1}{\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}}\\ =1\)
KK
26 tháng 8 2021
a. x2 - 2x
⇔ x(x - 2)
b. 3x - 6y
⇔ 3(x - 2y)
c. 5(x + 3y) - 15x(x + 3y)
⇔ (5 - 15x)(x + 3y)
d. 3(x - y) - 5x(y - x)
⇔ 3(x - y) + 5x(x - y)
⇔ (3 + 5x)(x - y)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 12 2021
a/
\(\frac{72}{\left(x-2\right)^2}=8\left(x\ne2\right)\Rightarrow\left(x-2\right)^2=9=3^2\)
\(\Rightarrow\left|x-2\right|=3\)
+ Nếu \(x-2\ge0\Rightarrow x\ge2\Rightarrow x-2=3\Rightarrow x=5\) (thoả mãn đk \(x\ge2\) )
+ Nếu \(x-2< 0\Rightarrow x< 2\Rightarrow2-x=3\Rightarrow x=-1\) (Thoả mãn đk \(x< 2\) )
b/
\(75-5\left(x-3\right)^3=700\Rightarrow\left(x-3\right)^3=-125=\left(-5\right)^3\)
\(\Rightarrow x-3=-5\Rightarrow x=-2\)
1/
PT $\Leftrightarrow \sin ^2x-(1-\sin ^2x)+\sin x-2=0$
$\Leftrightarrow 2\sin ^2x+\sin x-3=0$
$\Leftrightarrow (\sin x-1)(2\sin x+3)=0$
$\Leftrightarrow \sin x=1$ (chọn) hoặc $\sin x=-\frac{3}{2}< -1$ (loại)
Vậy $\sin x=1$
$\Leftrightarrow x=\frac{\pi}{2}+2k\pi$ với $k$ nguyên.
4/
ĐKXĐ: $\tan x\neq -1$
PT $\Rightarrow \cos ^2x(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin ^2x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin x)(1+\sin x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (\sin x+1)[(1-\sin x)(\cos x-1)-2(\sin x+\cos x)]=0$
$\Leftrightarrow (\sin x+1)(-1-\sin x\cos x-\sin x-\cos x)=0$
$\Leftrightarrow (\sin x+1)^2(\cos x+1)=0$
Nếu $\sin x=-1\Rightarrow x=\frac{-\pi}{2}+2k\pi$ với $k$ nguyên (tm)
Nếu $\cos x=-1\Rightarrow x=\pi +2k\pi$ với $k$ nguyên.