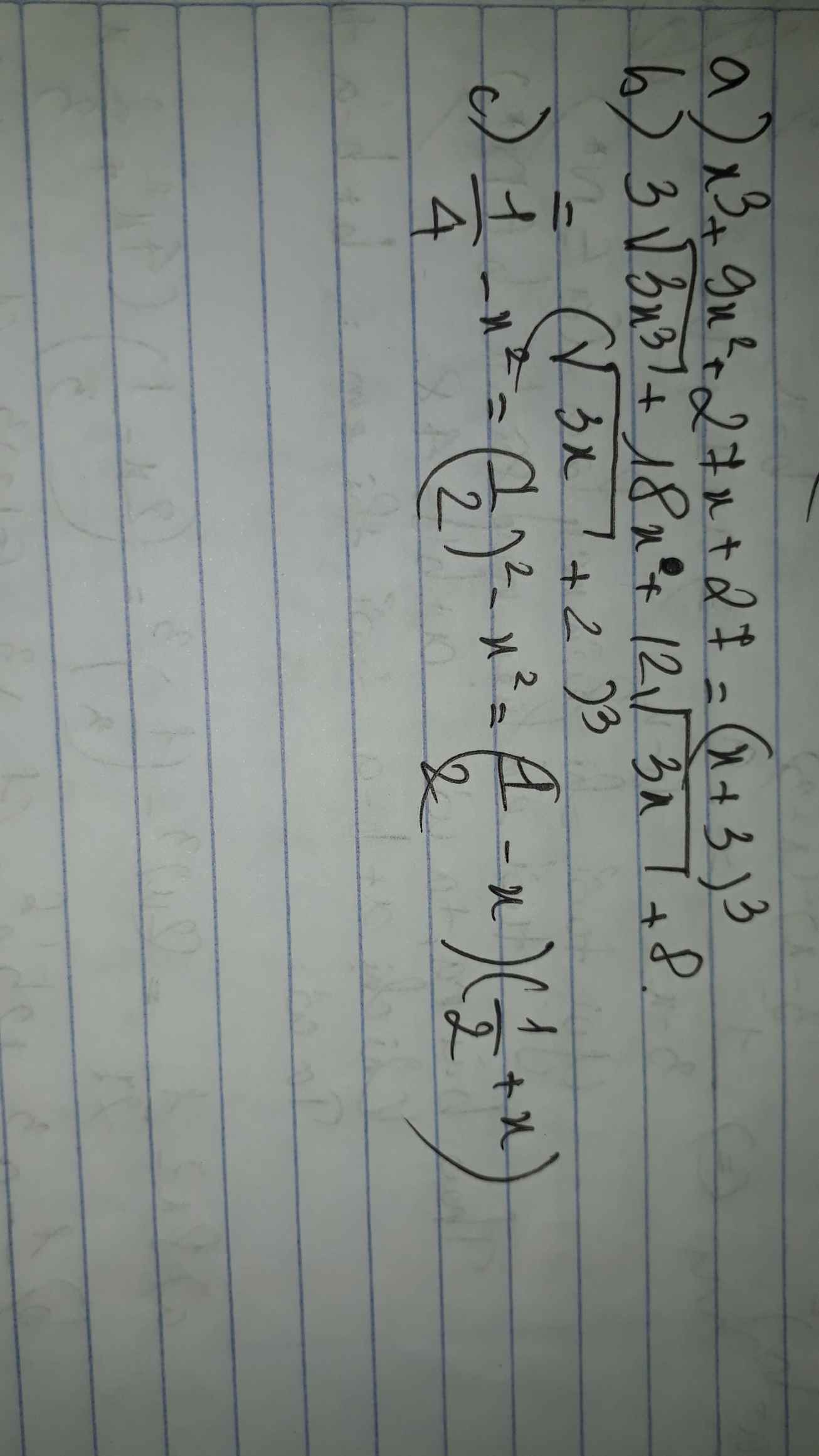phân tích đa thức sau thành nhân tử x^8+3x^4+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
3
25 tháng 5 2015
a) x8 + x + 1 = (x^2+x+1)*(x^6-x^5+x^3-x^2+1)
b) x^8 + 3x^4 + 4 = (x^4-x^2+2)*(x^4+x^2+2)
NT
3
16 tháng 7 2021
\(x^4-3x^3-x+3\)
\(=x^4-x^3-2x^3+2x-3x+3\)
\(=\)\(x^3\left(x-1\right)-2x\left(x^2-1\right)-3\left(x-1\right)\)
\(=x^3\left(x-1\right)-2x\left(x-1\right)\left(x+1\right)-3\left(x-1\right)\)
\(=\left[x^3-2x\left(x+1\right)-3\right]\left(x-1\right)\)
\(=\left[x^3-2x^2-2x-3\right]\left(x-1\right)\)
\(=\)\(\left[x^3-3x^2+x^2-3x+x-3\right]\left(x-1\right)\)
\(=\left[x^2\left(x-3\right)+x\left(x-3\right)+\left(x-3\right)\right]\left(x-1\right)\)
\(=\left[\left(x-3\right)\left(x^2+x+1\right)\right]\left(x-1\right)\)
QA
29 tháng 7 2021
Trả lời:
a, x4 + 3x3 + x2 + 3x
= ( x4 + 3x3 ) + ( x2 + 3x )
= x3 ( x + 3 ) + x ( x + 3 )
= ( x3 + x ) ( x + 3 )
= x ( x2 + 1 ) ( x + 3 )
b, Sửa đề: x4 - x2 + 8x - 8
= ( x4 - x2 ) + ( 8x - 8 )
= x2 ( x2 - 1 ) + 8 ( x - 1 )
= x2 ( x - 1 ) ( x + 1 ) + 8 ( x - 1 )
= ( x - 1 ) [ x2 ( x + 1 ) + 8 ]
= ( x - 1 ) ( x3 + x2 + 8 )
7 tháng 10 2021
a: \(x^4+x^2+2x+6\)
\(=x^4-2x^3+3x^2+2x^3-4x^2+6x+2x^2-4x+6\)
\(=\left(x^2-2x+3\right)\left(x^2+2x+2\right)\)
19 tháng 7 2021
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
KN
3 tháng 7 2019
\(x^8+3x^4+4\)
\(=\left(x^8-x^6+2x^4\right)+\left(x^6-x^4+2x^2\right)+\left(2x^4-2x^2+4\right)\)
\(=x^4\left(x^4-x^2+2\right)+x^2\left(x^4-x^2+2\right)+2\left(x^4-x^2+2\right)\)
\(=\left(x^4+x^2+2\right)\left(x^4-x^2+2\right)\)
KN
3 tháng 7 2019
\(4x^4+4x^3+5x^2+2x+1\)
\(=\left(4x^4+2x^3+2x^2\right)+\left(2x^3+x^2+x\right)+\left(2x^2+x+1\right)\)
\(=2x^2\left(2x^2+x+1\right)+x\left(2x^2+x+1\right)+\left(2x^2+x+1\right)\)
\(=\left(2x^2+x+1\right)^2\)
