Một tam giác có chu vi bằng 36cm,ba cạnh của nó tỉ lệ thuận với 3;4;5.Tính độ dài ba cạnh của tam giác đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 1 2022
Gọi độ dài 3 cạnh lần lượt là a,b,c (a,b,c>0)
Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{36}{12}=3\)
\(\dfrac{a}{3}=3\Rightarrow a=9\\ \dfrac{b}{4}=3\Rightarrow b=12\\ \dfrac{c}{5}=3\Rightarrow c=15\)
Vậy độ dài 3 cạnh tam giác lần lượt là 9, 12, 15 cm
3 tháng 1 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{36}{12}=3\)
Do đó: a=9; b=12; c=15
12 tháng 12 2021
Tham khảo theo đường link ( tại mik lười :v )
Một tam giác có chu vi bằng 36cm,ba cạnh của nó tỉ lệ thuận với 3;4;5.Tính độ dài ba cạnh của tam giác đó - Hoc24
DN
27 tháng 12 2021
Gọi độ dài ba cạnh của tam giác đó lần lượt là a ; b ; c ( cm, a ; b ; c \(\in\)N*)
Giả sử a < b < c
Vì độ dài 3 cạnh của tam giác đó tỉ lệ với 3 ; 4 ; 5
=> \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Áp dụng tích chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)( Vì chu vi của tam giác đó là 36 và a ; b ; c là độ dài 3 cạnh của tam giác đó)
Khi đó a = 3.3 = 9 cm ; b = 3.4 = 12 cm ; c = 3.5 = 15 cm
Vậy......
Học tốt
#Dương
18 tháng 8 2015
Gọi 3 cạnh của nó là a, b, c
Ta có:
a/3 = b/4 = c/5 và a + b + c = 36
Áp dụng tính chất dãy tỉ số bằng nhau, có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
Suy ra: a/3 = 3 => a = 3 . 3 = 9
b/4 = 3 => b = 4 . 3 = 12
c/5 = 3 => c = 5 . 3 =15
Vậy 3 cạnh đó lần lượt là: 9 ; 12 ; 15 (cm)
CM
17 tháng 5 2019
Gọi độ dài các cạnh của tam giác lần lượt là x, y, z
Theo đề bài ta có: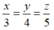 
và x + y + z = 36
Theo tính chất của dãy tỉ số bằng nhau ta có:
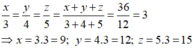
Chọn đáp án A
CC
18 tháng 12 2019
Gọi độ dài 3 cạnh của tam giác đó lần lượt là a, b, c \(\left(a,b,c\inℕ^∗;a,b,c< 36\right)\)
Ta có: \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
\(\Rightarrow a=9\), \(b=12\), \(c=15\)
Vậy độ dài 3 cạnh của tam giác lần lượt là \(9cm\), \(12cm\), \(15cm\)
TN
17 tháng 8 2015
a) goi a,b,c lan luot la 3 phan cua so18 ( a,b,c>0)
theo de bai ta co:
a,b,c ti le nghich voi 3;4;6
a+b+c=18
--> a.3=b.4=c.6 va a+b+c=18
--> \(\frac{a.3}{12}=\frac{b.4}{12}=\frac{c.6}{12}\)va a+b+c=18
-> \(\frac{a}{4}=\frac{b}{3}=\frac{c}{2}\)va a+b+c=18
Ap dung t/c day ti so bang nhau ta co
\(\frac{a}{4}=\frac{b}{3}=\frac{c}{2}\)=\(\frac{a+b+c}{4+3+2}=\frac{18}{9}=2\)
-> a/4=2 =>a=4.2=8
b/3=2->b=3.2=6
c/2=2->c=2.2=4
b) tuong tu
c) goi a,b,c ( m) lan luot la do dai 3 canh cua tam giacc(a,b,c>0)
theo de bai ta co
a,b,c ti le thuan 5,13,12 va a+b+c=156
--> \(\frac{a}{5}=\frac{b}{13}=\frac{c}{12}=\frac{a+b+c}{5+13+12}=\frac{156}{30}=\frac{26}{5}\)
--> a/5 =26/5--> a=26
b/13=26/5-> b=338/5
c/12=26/5-> c=312/5
Vay do dai 3 canh lan luot la 26cm ,338/5 cm, 312/5 cm
d) Goi a,b,c (cm) lan luot la do dai 3 canh cua tam giac do ( a,b,c>0)
theo de bai ta co:
a,b,c ti le nghich 8,9,12 va a+b+c=52
-> a.8=b.9=c.12 va a+b+c=42
-> \(\frac{a.8}{72}=\frac{b.9}{72}=\frac{c.12}{72}\)va a+b+c=52
->\(\frac{a}{9}=\frac{b}{8}=\frac{c}{6}\)va a+b+c=52
tu giai
TH
11 tháng 10 2021
tổng ti lệ của 3 cạnh là : 3+4+5=12
cạnh thứ nhất là : (36:12)*3=9
cạnh thứ hai là : ( 36:12)*4=12
cạnh thứ ba là : (36:12)*5=15
Đ/S:
nhớ cho mik nha
Gọi ba cạnh của tam giác lần lượt là a,b,c (a,b,c \(\ne0\),cm)
Vì a,b,c tỉ lệ thuận với 3,4,5
=> \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{36}{12}=3\)
=> \(\dfrac{a}{3}=3\Leftrightarrow a=9\)
=> \(\dfrac{b}{3}=4\Leftrightarrow b=12\)
=> \(\dfrac{c}{5}=3\Leftrightarrow c=15\)
Vậy độ dài ba cạnh của tam giác đó là: 9cm, 12cm, 15cm
Gọi độ dài ba cạnh của tam giác đó lần lượt là a,b,c ( cm, a,b,c ≠ 0 )
Vì độ dài ba cạnh tam giác tỉ lệ thuân với 3,4,5 nên:
Theo bài ra ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) và \(a+b+c=36\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{36}{12}=3\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{3}=3\Rightarrow a=9\left(TMđk\right)\\\dfrac{b}{4}=3\Rightarrow b=12\left(TMđk\right)\\\dfrac{c}{5}=3\Rightarrow c=15\left(TMđk\right)\end{matrix}\right.\)
Vậy ...........................