Cho tam giác ABC vuông tại A,có AB bằng 2/3 AC, đường cao AH=12cm
@tính AB,BH,CH
b) kẻ AM là đường trung tuyến tam giác ABC. Tính HM va MC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2021
a: Ta có: \(AB=\dfrac{2}{3}AC\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{4}{9}\)
\(\Leftrightarrow HB=\dfrac{4}{9}HC\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{4}{9}=144\)
\(\Leftrightarrow HC^2=324\)
\(\Leftrightarrow HC=18\left(cm\right)\)
\(\Leftrightarrow HB=8\left(cm\right)\)
\(\Leftrightarrow AB=\sqrt{8\cdot26}=4\sqrt{13}\left(cm\right)\)
CM
19 tháng 9 2019
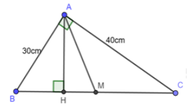
Áp dụng định lý Pytago cho ABH vuông tại A có:
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
Vì AM là đường trung tuyến M là trung điểm BC
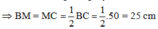
Ta có: MH = BM – BH = 25 – 18 = 7 cm
Đáp án cần chọn là: A
11 tháng 9 2016
BH = 18 cm ; MH = 7 cm ; MC = 25 cm ; AH = 24 cm. Chỉ có đáp án thôi nha!
20 tháng 11 2021
\(a,BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\\ HTL:\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=\dfrac{60}{13}\left(cm\right)\\BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\end{matrix}\right.\\ b,AM=\dfrac{1}{2}BC=\dfrac{13}{2}\left(cm\right)\left(trung.tuyến.ứng.cạnh.huyền\right)\\ \Rightarrow HM=\sqrt{AM^2-AH^2}=\dfrac{119}{26}\left(cm\right)\\ \Rightarrow S_{AHM}=\dfrac{1}{2}AH\cdot HM=\dfrac{1}{2}\cdot\dfrac{60}{13}\cdot\dfrac{119}{26}=\dfrac{1785}{169}\left(cm^2\right)\)
11 tháng 5 2023
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
AH=9*12/15=7,2cm
b: ΔHAB vuông tại H có HM vuông góc AB
nên MH^2=MA*MB
30 tháng 7 2019
VÌ AM LÀ ĐƯỜNG TRUNG TUYẾN ỨNG VỚI CẠNH HUYỀN
SUY RA AM=1/2*BC=1/2*10=5 CM
XÉT TAM GIÁC AHM VUÔNG TẠI H[VÌ AH LÀ ĐƯỜNG CAO]
SUY RA MH^2=AM^2-AH^2[PI TA GO]
MH^2=5^2-4,8^2
MH^2=1,96
MH=1,4
LẠI CÓ
BH=BM+MH=1/2*BC+1,4=5+1,4=6,4[CM]
TA CÓ:
CH=CM-MH=1/2BC-MH=5-1,4=3,6
TAM GIÁC ABH
AB^2=BH^2+AH^2
SUY RA AB^2=6,4^2+4,8^2=64 AB=8[CM]
TAM GIÁC ABC
AC^2=BC^2-AB^2
AC^2=10^2-8^2=36 AC=6[CM]
a, Ta có : \(AB=\frac{2}{3}AC\)
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{144}=\frac{1}{\left(\frac{2}{3}AC\right)^2}+\frac{1}{AC^2}\Leftrightarrow AC=6\sqrt{13}\)cm
=> \(AB=\frac{2}{3}.6\sqrt{13}=4\sqrt{13}\)cm
Theo định lí Pytago tam giác ABH vuông tại H
\(BH=\sqrt{AB^2-AH^2}=8\)cm
Theo định lí Pytago tam giác AHC vuông tại H
\(CH=\sqrt{AC^2-AH^2}=18\)cm
=> BC = HB + HC = 8 + 18 = 26 cm
b, Vì AM là đường trung tuyến tam giác ABC => BM = MC = BC / 2 = 13 cm
Ta có : BH + MH = BM => MH = BM - BH = 13 - 8 = 5 cm