1. Có hai hộp đựng cầu. Hộp 1 có 5 cầu đen và 10 cầu trắng; hộp 2 có 8 cầu đen và 15 cầu trắng. Lấy ngẫu nhiên 1 quả cầu từ hộp 1 bỏ sang hộp 2, sau đó từ hộp 2 lấy ngẫu nhiên ra 1 quả cầu. Tính xác suất để lấy được cầu trắng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
YCĐB tương đương với việc lấy ngẫu nhiên 2 cầu từ hộp 1 và 1 cầu từ hộp 2 đều trắng.
Xác suất lấy 2 cầu trắng từ hộp 1 là: $\frac{C^2_{10}}{C^2_{15}}=\frac{3}{7}$
Xác suất lấy 1 cầu trắng từ hộp 2 là: $\frac{C^1_7}{C^1_{15}}=\frac{7}{15}$
Xác suất lấy ngẫu nhiên 2 cầu từ hộp 1 và 1 cầu từ hộp 2 đều trắng là: $\frac{3}{7}.\frac{7}{15}=\frac{1}{5}$
HP
15 tháng 12 2021
a, Gọi T là biến cố "Trong 4 quả lấy ra có 3 quả cầu trắng".
\(\left|\Omega\right|=C^4_{15}\)
\(\left|\Omega_T\right|=C^3_7.C^1_8\)
\(\Rightarrow P\left(T\right)=\dfrac{\left|\Omega_T\right|}{\left|\Omega\right|}=\dfrac{C^3_7.C^1_8}{C^4_{15}}=\dfrac{8}{39}\)
CM
19 tháng 7 2018
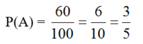
a) Không gian mẫu là kết quả của việc lấy ngẫu nhiên 1 quả cầu ở hộp thứ nhất và một quả cầu ở hộp thứ hai
+ Có 10 cách lấy 1 quả cầu bất kì ở hộp 1 và có 10 cách lấy 1 quả cầu bất kì ở hộp 2. Nên số phần tử của không gian mẫu là;
⇒ n(Ω) = 10.10 = 100.
A: “ Quả cầu lấy từ hộp thứ nhất trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 10 cách lấy quả cầu ở hộp B
⇒ n(A) = 6.10 = 60.
B: “Quả cầu lấy từ hộp thứ hai trắng”
⇒ Có 4 cách lấy quả cầu màu trắng ở hộp B và 10 cách lấy quả cầu ở hộp A
⇒ n(B) = 4.10 = 40.
A.B: “Cả hai quả cầu lấy ra đều trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 4 cách lấy quả cầu màu trắng ở hộp B
⇒ n(A.B) = 6.4 = 24.
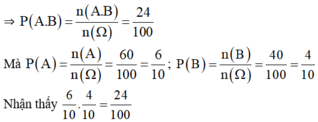
hay P(A.B) = P(A).P(B)
⇒ A và B là biến cố độc lập.
b) Gọi C: “Hai quả cầu lấy ra cùng màu”.
Ta có: A− : “Quả cầu lấy ra từ hộp thứ nhất màu đen”
B− : “ Quả cầu lấy ra từ hộp thứ hai màu đen”
⇒A−.B− : “Cả hai quả cầu lấy ra đều màu đen”
Nhận thấy A.B và A−.B− xung khắc (Vì không thể cùng lúc xảy ra hai trường hợp 2 quả cầu lấy ra cùng trắng và cùng đen)
Và C=(A.B)∪(A−.B−)
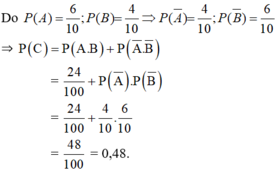
c) C− : “Hai quả cầu lấy ra khác màu”
⇒ P(C− )=1-P(C)=1-0,48=0,52
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2021
Không gian mẫu: \(C_{10}^3\)
a. Xác suất: \(\dfrac{C_4^2.C_6^1}{C_{10}^3}=...\)
b. \(P=\dfrac{C_4^2C_6^1+C_4^3}{C_{10}^3}=...\)
c. \(P=\dfrac{C_6^3}{C_{10}^3}=...\)
HP
7 tháng 12 2021
a, Gọi A là biến cố "Lấy ra bốn quả cùng màu".
\(\Rightarrow\left|\Omega\right|=C^4_{12}\)
\(\left|\Omega_A\right|=C^4_7+C^4_5\)
\(\Rightarrow P\left(A\right)=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{C^4_7+C^4_5}{C^4_{12}}=\dfrac{8}{99}\)
HP
7 tháng 12 2021
b, Gọi B là biến cố "Lấy ra một quả màu đen".
\(\Rightarrow\overline{B}\) là biến cố "Không lấy ra quả màu đen nào".
\(\Rightarrow\left|\Omega\right|=C^4_{12}\)
\(\left|\Omega_{\overline{B}}\right|=C^4_7\)
\(\Rightarrow P\left(\overline{B}\right)=\dfrac{C^4_7}{C^4_{12}}=\dfrac{7}{99}\)
\(\Rightarrow P\left(B\right)=1-P\left(\overline{B}\right)=\dfrac{92}{99}\)
