Cho hình vuông ABCD. Trên tia đối của tia CB lấy điểm M, trên tia đối của tia
DC lấy điểm N sao cho DN = BM. Đường thẳng song song với AN kẻ từ M và đường
thẳng song song với AM kẻ từ N cắt nhau ở điểm F.
a) Chứng minh tứ giác ANFM là hình vuông
b) Chứng minh rằng điểm F nằm trên đường phân giác của góc MCN
c) Chứng minh AC ┴ CF
d) Gọi O là trung điểm của AF. Chứng minh rằng ba điểm B,D,O thẳng hành và tứ
giác BOFC là hình thang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta\)ABM và \(\Delta\)ADN có: ^ABM = ^ADN (=900); AB=AD; BM=DN => \(\Delta\)ABM = \(\Delta\)ADN (c.g.c)
=> AM=AN (2 canh tương ứng); ^BAM = ^DAN (2 góc tương ứng). Mà ^BAM + ^DAM = 900
=> ^DAN + ^DAM = ^MAN = 900 => AM vuông góc AN
Ta có: MF//AN; NF//AM; AM vuông góc AN nên ^MAN = ^AMF = ^ANF = 900
Do đó: Tứ giác ANFM là hình chữ nhật. Lại có: AM=AN (cmt) => Tứ giác ANFM là hình vuông (đpcm).
b) Gọi I và J lần lượt là hình chiếu của F trên 2 đường thẳng CD và BC
Tứ giác ANFM là hình vuông => FM=FN
Xét tứ giác CNFM có: ^MCN = ^MFN = 900 => ^FNC + ^CMF = 1800 => ^FNC = ^FMJ hay ^FNI = ^FMJ
Xét \(\Delta\)FIN và \(\Delta\)FJM có: ^FIN = ^FJM (=900); FN=FM; ^FNI = ^FMJ
=> \(\Delta\)FIN = \(\Delta\)FJM (Ch.gn) => FI = FJ (2 cạnh tương ứng)
Xét ^MCN: Có FI và FJ là k/c từ điểm F tới 2 cạnh của góc này; FI=FJ
=> F nằm trên đường phân giác của ^MCN (đpcm).
c) Gọi giao điểm của tia AD và CF là E.
CF là phân giác ^MCN => ^FCN = ^MCN/2 = 450 => ^FCN = ^ACD = 450
=> \(\Delta\)ACE vuông tại C có đường phân giác CD. Mà CD vuông góc AE
=> \(\Delta\)ACE vuông cân tại C = >CD đồng thời là đường trung tuyến => D là trung điểm AE
Suy ra: OD là đường trung bình \(\Delta\)FAE => OD // EF hay OD // CF (1)
Dễ c/m: BD // CF (Do ^DBC + ^BCF = 450 + 1350 = 1800) (2)
Từ (1) và (2) => 3 điểm B;D;O thẳng hàng (đpcm).
d) Ta thấy: B;D;O là 3 điểm thẳng hàng; BD cố định nên O luôn thuộc đường thẳng BD cố định khi M di động trên Cx.

a, Theo giả thiết : AM//NF và AN//MF => ANFM là hình bình hành (1)
mà AD = AB; DN = BM => tg vuông ADN = tg vuông ABM => AN = AM (2)
và ^AND = ^AMB => AN _I_ AM (3) ( vì đã có DN _I_ BM)
(1) và (2) => ANFM là hình thoi (4)
(3) và (4) => ANFM là hình vuông
b, Gọi P và giao điểm của AM và CN. Dễ thấy tg vuông ANP đồng dạng tg vuông CMP ( vì có ^P đối đỉnh ) => AP/CP = AN/CM = FM/CM (5) (vì FM = AN)
Mặt khác : AP _I_ FM ( vì ANFM là hình vuông ) và CP _I_ CM => ^APC = ^FMC (6) ( góc có cạnh tương ứng vuông góc )
(5) và (6) => tg APC đồng dạng tam giác FMC => ^FCM = ^ACP = 45o = ^FCN => CF là tia phân giác của ^MCN và ^ACF = 90o
c, Dễ thấy AO/AM = AD/AC = √2 (7)
và vì ^OAM = ^DAC = 45o <=> ^OAM - ^DAM = ^DAC - ^DAM <=> ^OAD = ^MAC (8)
(7) và (8) => tg AOD đồng dạng tg AMC => ^ADO = ^ACM = 135o => ^ODN = 45o = ^BDC => B; D; O thẳng hàng
Dễ thấy BO//CF => BOFC là hình thang

\(\left(1-a+a^2\right)\left(1-b+b^2\right)=1-b+b^2-a+ab-ab^2+a^2-a^2b+a^2b^2.\)
\(=\frac{2-2a-2b+2b^2+2ab+2a^2-2ab\left(a+b\right)+2a^2b^2}{2}\)\(=\frac{\left(a-b\right)^2+1+a^2b^2+\left(1-a\right)^2\left(1-b\right)^2}{2}\ge\frac{1+a^2b^2}{2}\)
Tương Tự : \(\left(1-c+c^2\right)\left(1-d+d^2\right)\ge\frac{1+c^2d^2}{2}\)
(1-a+a2) (1-b+b2) = 1-b+b2-a+ab-ab2+a2-a2b+a2b2.
=2-2a-2b+2b2+2ab+2a2-2ab(a+b)+2a2b2 =(a-b)2+1+a2b2+(1-a)2(1-b)2> 1+a2b2 2 2 Tương Tự:(1-c+c2) (1-d+d2) > 1+c2d2 2


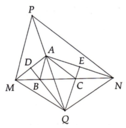

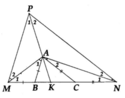
(Đề là trên tia BC nha)
â) Xét tam giác ABM va tam giac ADN ( ABM = ADN=90) , co :
BM=DN(gt)
AD=AB(ABCD là hinh vuông)
=> tam giac ABM = tam giac ADN (cgv-cgv)
=>AN=AM va MAB = NAD
Ta co : MAB + DAM=90
Ma MAB =NAD (cmt)
=>NAD + DAM =90
<=> NAM =90
Xet tg ANFM , co : AN//FM (gt) va AM//NF (gt)
=> ANFM la hbh
Ma NAM =90 (cmt) ; AN=AM (cmt)
=> ANFM là hình vuông ( Vì đây là hình chữ nhật có 2 cạnh kề bằng nhau )
b) Từ F kẻ FP vuông góc với NC , FH vuông góc với BC
Xét tam giác NPF và tam giác MHF (APF =HMF) , co :
MF = FN (AMFN la hinh vuong )
NFP=MFH ( cùng phụ với PFM )
=> tam giác NPF = tam giác MHF (c.huyen-gn)
=> PF=FH
Theo định lý đảo của tia phân giác trong NCM , co :
PF=FH(cmt)
Ma PF \(\perp\) PC (cách ve ) ; FH \(\perp\) CH
=> F nằm trên tia phân giác của NCM
c)Nói C và F , ta được CF là tia phân giác của NCM (câu b)
Ta có : PCF + FCH =PCH =90
Mà PCF = FCH ( CF là tia phân giác NCM)
=> PCH = 2 PCF (1)
Ta co : ACD + ACB = DCB =90
Mà ACD = ACB ( AC là tia phân giác DCB ; ABCD là hình vuông )
=> DCB = 2 ACD (2)
Từ (1) vả (2) => PCH + DCB = 2( PCF + ACD)
<=> 180 = 2 ( PCF + ACD)
<=> 180 = 2 . ACF
<=> ACF = 90
=>AC \(\perp\) CF( dpcm )
đ) Gọi R là giao điểm của hai đường chéo tg ABCD là AC và BD
Xét tam giác AFC , co :
OA =OF ( gt)
AR = CR ( do 2 đường chéo AC và BD cắt nhau tại trung điểm mỗi đường trong hình vuông ABCD )
=> OR là đường trung bình của tam giác AFC
=> O và R cùng thuộc 1 đường thẳng
Mặt khác , ta có : R \(\in\) BD ( cach ve )
=> O \(\in\) BD
=> O , B, D thẳng hàng
Ta có : OB //FC ( OR là đường trung bình )
=> BOFC là hình thang