Tính
x4 + 2007x2 + 2006x +2007
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 8 2017
có phải viết như này k ạ
A=\(x^6-2017.x^5..............\)
hya viết A= x.6-2017.x.5
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
NT
11
10 tháng 4 2018
213 x 37 + 213 x 37 + 23 x 213 + 213
= 213 x 37 + 213 x 37 + 23 x 213 + 213 x 1
= 213 x ( 37 + 37 + 23 + 1 )
= 213 x 98
= 20874
2007 x 16 - 2007 x 14 - 2007 x 2 + 2007
= 2007 x 16 - 2007 x 14 - 2007 x 2 + 2007 x 1
= 2007 x ( 16 - 14 - 2 - 1 )
= 2007 x 9
= 18063
Chúc bạn học tốt~
EC
5
17 tháng 2 2017
\(a,24\times4+24\times3+24\times2\)
\(=24\times\left(4+3+2\right)\)
\(=24\times9\)
\(=216\)
\(b,2007\times16-2007\times14-2007\times2+2007\)
\(=2007\times\left(16-14-2+1\right)\)
\(=2017\times1\)
\(=2017\)
17 tháng 2 2017
a, 24 x ( 4 + 3 + 2 ) = 24 x 9 = 216
b, 2007 x 16 - 14 - 2 + 1 ) = 2007 x 1 = 2007
đúng r
PT
1
CM
19 tháng 3 2018
Đáp án B
Cách 1: Tư duy suy luận
Ta có
L = lim x → + ∞ m x + 2006 x + x 2 + 2007 = lim x → + ∞ x m + 2006 x x + x 1 + 2007 x 2 = lim x → + ∞ x m + 2006 x x 1 + 1 + 2007 x 2
= lim x → + ∞ m + 2006 x 1 + 1 + 2007 x 2 = m 1 + 1 = m 2 . Để L=0 thì m 2 = 0 ⇔ m = 0 .
Cách 2: Sử dụng máy tính cầm tay
Chọn m=0,5 thỏa mãn các phương án A, C, D. Ta có L = lim x → + ∞ 0,5 x + 2006 x + x 2 + 2007 .
Nhập vào màn hình:
Suy ra L ≈ 1 4 ⇒ L ≠ 0 . Loại ngay A, C, D.
DV
2
TL
4 tháng 2 2019
đặt tổng trên là A
có (2006x-2007)^2008>=0
và (2008y+2009)^2010>=0
từ các điều kiện trên =>A>=0
MÀ ĐỀ BÀI BẮT TÌM A=<0
TỪ 2 ĐIỀU KIỆN TRÊN =>A CHỈ CÓ THỂ =0
(=)(2006x-2007)^2008=0 và (2008y+2009)^2010=0
(=) 2006x-2007=0 và 2008y+2009=0
(=)2006x=2007 và 2008y=2009
(=)x=2007/2006 và y=2009/2008
vậy x=2007/2006 và y=2009/2008
LN
4 tháng 2 2019
Vì \(\hept{\begin{cases}\left(2006x-2007\right)^{2008}\ge0;\forall x\\\left(2008x+2009\right)^{2010}\ge0;\forall y\end{cases}}\)
\(\Rightarrow\left(2006x-2007\right)^{2008}+\left(2008x+2019\right)^{2010}\ge0;\forall x;y\)
Đẳng thức xảy ra khi :
\(\hept{\begin{cases}2006x-2007=0\\2008x+2009=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{2007}{2006}\\y=\frac{-2009}{2008}\end{cases}}\)
Vậy \(x=\frac{2007}{2006};y=\frac{-2009}{2008}\)
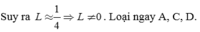
\(x^4+2007x^2+2006x+2007\)
\(=x^4+2007x^2+2007x-x+2007\)
\(=\left(x^4-x\right)+\left(2007x^2+2007x+2007\right)\)
\(=x\left(x^3-1\right)+2007\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x^2+x+1\right)+2007\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^2-x+2007\right)\)