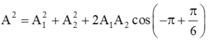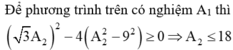Một vật thực hiện đồng thời hai dao động điều hòa x1=A1cos(wt+pi/3) (cm), x2=A2cos(wt-pi/2) (cm). Biết biên độ của dao dộng là 8cm. Tìm A1 để A2 đạt giá trị lớn nhất. Tính pha ban đầu của dao động tổng hợp lúc đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
14 tháng 6 2017
Vật có m=200g thực hiện đồng thời 2 dao động điều hòa có phương trình x1=4cos10t(cm) và x2=6cos(10t). Tính lực tác dụng cực đại gây ra cho dao động tổng hợp của vật.
Lời giải:
Dao động tổng hợp: x = x1 + x2 = 10 cos(10t) (cm)
Lực tác dụng gây dao động cho vật: \(F=-k.x=-m\omega^2.x\)
\(\Rightarrow F_{max}=m.\omega^2.A=0,2.10^2.0,1=2(N)\)
HD
Hà Đức Thọ
Admin
14 tháng 6 2017
1 vật có m=100g thực hiện đồng thời 2 dao động điều hòa cùng phương cùng tần sói f=10Hz , biên độ A1=8cm,phi1= pi/3 ; A2=8cm, phi2= -pi/3 . Biểu thức thế năng của vật theo thời gian là
A. Wt=1,28sin^2(20pi×t)(J)
B. Wt=2,56sin^2(20pi×t) (J)
C. Wt=1,28cos^2(20pi×t)(J)
D. Wt=1280sin^2(20pi×t)(J)
Lời giải:
\(\omega =2\pi.f = 20\pi (rad/s)\)
\(x_1=8\cos(20\pi t + \dfrac{\pi}{3})\)
\(x_2=8\cos(20\pi t - \dfrac{\pi}{3})\)
Suy ra dao động tổng hợp là: \(x=8\cos(20\pi t)(cm)\)
Thế năng: \(W_t=\dfrac{1}{2}k.x^2=\dfrac{1}{2}m\omega^2.x^2\)
\(\Rightarrow W_t=\dfrac{1}{2}.0,1.(20\pi)^2.0,08^2.\cos^2(20\pi t)\)
\(=1,28\cos^2(20\pi t)\)(J)
Chọn C.
HY
12 tháng 3 2015
\(x_1 = 5 \cos (\omega t + \varphi)cm.\)
\(x_2 = A_2 \cos (\omega t - \frac{\pi}{4})cm.\)
\(x= A \cos (\omega t - \frac{\pi}{12})cm.\)
Vẽ giản đồ véc tơ như hình vẽ
Áp dụng định lý hàm số Sin ta có:
Xét: \(\triangle OA_1A:\) \(\frac{A}{\sin OA_1A} = \frac{A_1}{\sin OAA_1} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_1}{\sin (\frac{\pi}{6})} \)
=> \(A= \frac{A_1}{\sin (\frac{\pi}{6})} .\sin (\frac{3\pi}{4}-\varphi).(*)\)
TH1: \(A= A _{max} <=> \sin (\frac{3\pi}{4}-\varphi) = 1\)
=> \(A_{max}= \frac{A_1}{\sin (\frac{\pi}{6})}= 10cm.(1)\)
TH2: \(A = \frac{A_{max}}{2} => \sin (\frac{3\pi}{4}-\varphi) = \frac{1}{2}.\)
=> \(\frac{3\pi}{4} - \varphi = \frac{\pi}{6}\)
=> \(\varphi = \frac{7\pi}{12}.(2)\)
Xét: \(\triangle OA_2A:\) \(\frac{A}{\sin OA_2A} = \frac{A_2}{\sin OAA_2} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_2}{\sin (\varphi+\frac{\pi}{12})} \)
=> \(A_2= \frac{A_{max}}{\sin (\frac{3\pi}{4}-\varphi)} .\sin (\frac{\pi}{12}+\varphi).(3)\)
Thay \((1); (2)\) vào \((3)\) ta được: \(A_2= \frac{10}{0,5} .\sin (\frac{\pi}{12}+\frac{7\pi}{12}) = \frac{10}{0,5}.\frac{\sqrt{3}}{2} = 10 \sqrt{3}cm.\)
Chọn đáp án.C.\(10\sqrt{3}cm.\)
19 tháng 1 2018
Coi chừng sai đề ấy chứ nếu o sai mn giúp bn tl rùi xem lại nhen!!
VT
13 tháng 7 2017
Chọn đáp án C
A t 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos φ ⇔ 20 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos 11 18 π
⇒ 20 2 = A 1 + A 2 2 − 2 , 68. A 1 A 2 ≥ A 1 + A 2 2 − 2 , 68. A 1 + A 2 2 4 = 0 , 33 A 1 + A 2 2
⇒ A 1 + A 2 ≤ 34 , 9 c m .
