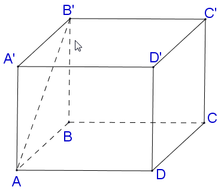
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là tứ giác đều cạnh a biết rằng BD′=a√6. Tính thể tích của lăng trụ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)
20 tháng 10 2021
\(AA'=\dfrac{2a}{\sqrt{3}}\)
\(V=AA'\cdot S_{ABCD}=\dfrac{16a^3}{\sqrt{3}}\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 8 2021
\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)
