cho tam giác abc cân tại a có góc a nhọn. gọi h là trực tâm của tâm giác và góc hba=30 độ. Xét 2 khẳng định sau:
A. tam giác ABC vuông cân
B. tam giác ABC đều
giải thịch và chọn đáp án đúng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 9 2018
Đáp án D
Ta có: B C ⊥ A A ' B C ⊥ A H
Do đó:
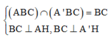
Mặt khác, tam giác A’BC vuông cân tại A’
nên A ' H = 1 2 B C = 3 a 2
Ta có:
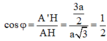
⇒ φ = 60 o
14 tháng 4 2023
1: góc ADC=góc AEC=90 độ
=>ADEC nội tiếp
2: góc ABH=90 độ-góc BAC=góc DEA
10 tháng 5 2023
a: Xét ΔAKB và ΔAKC có
AB=AC
góc BAK=góc CAK
AK chung
=>ΔAKB=ΔAKC
ΔABC cân tại A
mà AK là phân giác
nên AK vuông góc CB
b: Xét ΔACB có
BM,AK là trung tuyến
BM cắt AK tại G
=>G là trọng tâm
c: BK=CK=18/2=9cm
=>\(AK=\sqrt{30^2-9^2}=3\sqrt{91}\left(cm\right)\)
=>\(AG=2\sqrt{91}\left(cm\right)\)
CM
2 tháng 1 2019
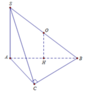
Đáp án D
Vì B C ⊥ S A B C ⊥ C A ⇒ B C ⊥ S A C ⇒ B C ⊥ S C ⇒ O là tâm đường tròn ngoại tiếp tam giác SBC
Vì S A ⊥ A B C ⇒ H là trung điểm của AB
a: Vì góc A nhọn nên chắc chắn tam giác ABC không thể vuông cân
=> Loại
b: Gọi giao điểm của BH và AC là K
=> BK\(\perp\)AC tại K
Ta có: ΔABK vuông tại K
nên \(\widehat{ABK}+\widehat{BAK}=90^0\)
hay \(\widehat{BAC}=60^0\)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)
nên ΔABC đều
bạn giúp mk câu nữa được k ạ