Cho \(\Delta ABC=\Delta DEF\). Biết \(\widehat{A}=55^0,\widehat{E}=75^0\)
Tính các góc còn lại của mỗi tam giác ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2016
1/ Ta có: tam giác ABC = tam giác DEF
=> góc A = góc D
góc B = góc E
góc C = góc F
Ta có: góc A + góc B + góc C = 1800
1300 + góc C = 1800
góc C = 1800-1300 = 500
Ta có: góc A + góc B = 1300
góc A + 550 = 1300
góc A = 1300 - 550 =750
Vậy góc A = góc D = 750
góc B = góc E = 550
góc C = góc F = 500
2/ Ta có: tam giác DEF = tam giác MNP
=> DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10 cm
Mà NP - MP = EF - FD = 2 cm
EF = (10 + 2) : 2 = 6 (cm)
FD = (10 - 2) : 2 = 4 (cm)
Vậy DE = MN = 3 cm
EF = NP = 6 cm
FD = MP = 4 cm
AT
7 tháng 11 2016
1) Ta có: ( \(\widehat{A}\) + \(\widehat{B}\)) + \(\widehat{C}\) = 180o
hay 130o + \(\widehat{C}\) = 180o
\(\Rightarrow\) \(\widehat{C}\) = 180o - 130o = 50o
Vì ΔABC = ΔDEF nên ta có:
\(\widehat{C}\) = \(\widehat{F}\) = 50o
\(\widehat{E}\) = \(\widehat{B}\) = 55o
Ta có: \(\widehat{A}\) + \(\widehat{B}\) = 130o hay \(\widehat{A}\) + 55o = 130o
\(\Rightarrow\) \(\widehat{A}\) = 130o - 55o = 75o
\(\Leftrightarrow\) \(\widehat{A}\) = \(\widehat{D}\) = 75o
Vậy: \(\widehat{A}\) = \(\widehat{D}\) = 75o
\(\widehat{B}\) = \(\widehat{E}\) = 55o
\(\widehat{C}\) = \(\widehat{F}\) = 50o
2) ΔDEF = ΔMNP nên:
\(\Rightarrow\) DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10cm
mà ΔDEF = ΔMNP
\(\Rightarrow\) NP - MP = EF - FD = 2cm
\(\Rightarrow\) EF = \(\frac{10+2}{2}\) = 6cm
FD = 6cm - 2cm = 4cm
Vậy: DE= MN = 3cm
EF = NP = 6cm
FD = PM = 4cm
HM
10 tháng 7 2017
trời ạ
ta có tam giác ABC= tam giác DEF
suy ra góc A = góc D , góc b = góc E , góc C = góc F
trong tam giác ABC CÓ góc A + góc B +góc C = 180 độ
mà góc A=55 độ , B = 75 độ
suy ra góc C =50 độ
mà góc C = góc F = 50 độ
góc D = góc A =55 độ
góc B = góc E = 75 độ
cho mình nha
thanhks
10 tháng 7 2017
giải
Ta có : \(\Delta ABC=\Delta DEF\)
\(\Rightarrow\widehat{A}=\widehat{D}=55^0\)
\(\widehat{B}=\widehat{E}=75^0\)
Ta có tổng 3 góc trong một tam giác bằng 1800
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)=180^0-\left(55^0+75^0\right)\)
\(\Rightarrow\widehat{C}=\widehat{F}=50^0\)
5 tháng 12 2021
\(\Delta ABC=\Delta DEF\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=\widehat{D}=55^0\\\widehat{E}=\widehat{B}=75^0\end{matrix}\right.\\ \Rightarrow\widehat{C}=\widehat{F}=180^0-\widehat{A}-\widehat{B}=50^0\)
5 tháng 11 2016
Ta có: tam giác ABC = tam giác DEF.
=> góc A = góc D = 55 độ
góc B = góc E = 75 độ
góc C = góc F
Trong tam giác ABC ta có:
góc A + góc B + góc C = 180* (tổng 3 góc của tam giác)
55* + 75* + góc C = 180*
góc C = 180* - (55*+75*)
góc C = 180* - 130* = 50*
Vậy góc A = góc D = 55 độ
góc B = góc E = 75 độ
góc C = góc F = 50*
31 tháng 1 2021
Ta có tam giác ABC= tam giác DEF Có góc A = 55 độ ; Góc E =75 độ => Góc A = 55 độ , D = 55 độ => Góc E = 75 độ ; Góc B = 75 độ Xét tam giác ABC có : A+B+C=180 độ =>góc C= 180 - (Góc A+ góc B) =>gócC=180- 130= 50 độ
=> góc C = 50 độ
HP
2 tháng 11 2015
ta có tam giác ABC=tam giác DEF
có góc A=55 độ;góc E=75 độ
tam giác ABC=tam giác DEF,góc A=55 độ
=>góc A=góc D=55 độ
góc E=75 độ=>góc E=góc B=75 độ
xét tam giác ABC có:A+B+C=180 độ
=>góc C=180 -(góc A+góc B)
=>góc C=50 độ
Vì tam giác ABC=tam giác DEF,góc C=50 độ
=>góc F=góc C=50 độ
vậy ....
tick nha các bạn
TT
20 tháng 4 2017
Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
20 tháng 4 2017
Giải:
Xem hình vẽ
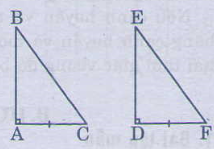
* Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
6 tháng 8 2019
\(\widehat{C}=\frac{5}{6}\widehat{B}\Rightarrow\widehat{\frac{C}{5}}=\frac{\widehat{B}}{6}\)
Mà \(\Delta ABC=\Delta DEP\)\(\Rightarrow\widehat{E}=\widehat{B}\) và \(\widehat{C}=\widehat{F}\) ( Hai cặp góc tương ứng )
Mà \(\widehat{E}-\widehat{F}=10^o\Rightarrow\widehat{B}-\widehat{C}=10^o\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{\widehat{B}}{6}=\frac{\widehat{C}}{5}=\frac{\widehat{B}-\widehat{C}}{6-5}=\frac{10^o}{1}=10^o\)
Có : \(\frac{\widehat{B}}{6}=10^o\Rightarrow\widehat{B}=10^o.6=60^o\)
\(\frac{\widehat{C}}{5}=10^o\Rightarrow\widehat{C}=10^o.5=50^o\)
Mà \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{A}+60^o+50^o=180^o\)
\(\Rightarrow\widehat{A}=180^o-60^o-50^o=70^o\)
Lại có : \(\widehat{A}=\widehat{D}=70^o;\widehat{B}=\widehat{E}=60^o;\widehat{C}=\widehat{F}=50^o\)
Kết luận ...
Vì \(\Delta ABC=\Delta DEF\) nên \(\widehat{A}\) = \(\widehat{D}\) = \(55^o\)
Ta có : \(\widehat{D}\) + \(\widehat{E}\) + \(\widehat{F}\) = \(180^o\)
\(\widehat{F}\) = \(180^o\) - \(\widehat{D}\) - \(\widehat{E}\)
\(\widehat{F}\) = \(180^o\)- \(55^o\) - \(75^o\)
\(\widehat{F}\) = \(50^o\)
Vì \(\Delta ABC=\Delta DEF\) nên \(\widehat{B}\) = \(\widehat{E}\) = \(75^o\)
B=75
D=55
C=40
F=40