chứng tỏ E <3/16
E=1/3-2/3^2+3/3^3-4/3^4+...+2015/3^2015-2016/3^2016
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=> \(4E=4+4^2+4^3+...+4^{12}\)
=> \(3E=4E-E=4^{12}-1\)
2. => 3E = 412 - 1 < 412

bạn tự vẽ hình nhé
a) trên tia by có bk > bh ( 8cm > 5cm )
=> h nằm giữa b và k
b) vì h nằm giữa b và k
=> bh + hk = bk
=> 5 + hk = 8
=> hk = 8 - 5
=> hk = 3 ( cm )
trên tia by có be < bh ( 2cm > 5 cm )
=> e nằm giữa b và h
=> be + eh = bh
=> 2 + eh = 5
=> eh = 5 - 2
=> eh = 3 ( cm ) mà hk = 3 cm
=> e nằm giữa b và h
vì h nằm giữa e và k mà e nằm giữa b và h
=> h là trung điểm của ek
bn cứ làm như thế nhé
bạn tự vẽ hình nhé
a) trên tia by có bk > bh ( 8cm > 5cm )
=> h nằm giữa b và k
b) vì h nằm giữa b và k
=> bh + hk = bk
=> 5 + hk = 8
=> hk = 8 - 5
=> hk = 3 ( cm )
trên tia by có be < bh ( 2cm > 5 cm )
=> e nằm giữa b và h
=> be + eh = bh
=> 2 + eh = 5
=> eh = 5 - 2
=> eh = 3 ( cm ) mà hk = 3 cm
=> e nằm giữa b và h
vì h nằm giữa e và k mà e nằm giữa b và h
=> h là trung điểm của ek


a) ΔADB và ΔABC vuông có ∠B chung ∠ ΔADB ∼ ΔCAB (g.g)
b) Vì ∠B = 2∠C (gt) ∠ ∠B1 = ∠B2 = ∠C
Do đó hai tam giác vuông ABE và ACB đồng dạng (g.g)
![]()
c) Ta có ΔADB ∼ ΔCAB (cmt)
![]()
Theo tính chất đường phân giác ta có :

d) Ta có AB = 2BD (gt)
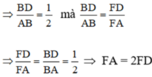
![]()


1: H đối xứng D qua AB
=>AH=AD: BH=BD
=>ΔAHD cân tại A
=>AB là phân giác của góc HAD(1)
H đối xứng E qua AC
=>AH=AE: CH=CE
=>ΔAHE cân tại A
=>AC là phân giác của góc HAE(2)
Từ (1), (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
Xet ΔAHB và ΔADB có
AH=AD
BH=BD
AB chung
=>ΔAHB=ΔADB
=>góc ADB=90 độ
=>BD vuông góc DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
HC=EC
AC chung
=>ΔAHC=ΔAEC
=>góc AEC=90 độ
=>CE vuông góc DE(4)
Từ (3), (4) suy ra BD//CE
3: BD*CE=BH*CH=AH^2=DE^2/4


có BC và AE là 2 đường chéo giao tại m
mà m là trung ddierm của BC ( đề bài )
m là trung điểm AE ( tia đối )
=> ABCE là hình bình hành
=> AB = CE và AC //BE
------------ VIẾT THÊM HÌNH CHỮ E VÀO MK QUÊN CH VIẾT ĐÓ --------------
\(E=\dfrac{1}{3}-\dfrac{2}{3^2}+\dfrac{3}{3^3}-\dfrac{4}{3^4}+...+\dfrac{2015}{3^{2015}}-\dfrac{2016}{3^{2016}}\\ 3E=1-\dfrac{2}{3}+\dfrac{3}{3^2}-\dfrac{4}{3^3}+...+\dfrac{2015}{3^{2014}}-\dfrac{2016}{3^{2015}}\\ 3E+E=\left(1-\dfrac{2}{3}+\dfrac{3}{3^2}-\dfrac{4}{3^3}+...+\dfrac{2015}{3^{2014}}-\dfrac{2016}{3^{2015}}\right)+\left(\dfrac{1}{3}-\dfrac{2}{3^2}+\dfrac{3}{3^3}-\dfrac{4}{3^4}+...+\dfrac{2015}{3^{2015}}-\dfrac{2016}{3^{2016}}\right)\\ 4E=1-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{2014}}-\dfrac{1}{3^{2015}}-\dfrac{2016}{3^{2016}}\\ 12E=3-1+\dfrac{1}{3}-\dfrac{1}{3^2}+...+\dfrac{1}{3^{2013}}-\dfrac{1}{3^{2014}}-\dfrac{6048}{3^{2016}}\\ 4E+12E=\left(3-1+\dfrac{1}{3}-\dfrac{1}{3^2}+...+\dfrac{1}{3^{2013}}-\dfrac{1}{3^{2014}}-\dfrac{2016}{3^{2015}}\right)+\left(1-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{2014}}-\dfrac{1}{3^{2015}}-\dfrac{2016}{3^{2016}}\right)\\ 16E=3-\dfrac{2017}{3^{2015}}-\dfrac{2016}{3^{2016}}\\ 16E=3-\left(\dfrac{2017}{3^{2015}}+\dfrac{672}{3^{2015}}\right)\\ 16E=3-\dfrac{2689}{3^{2015}}< 3\\ \Rightarrow E< \dfrac{3}{16}\)