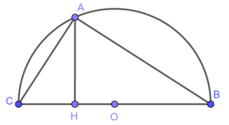
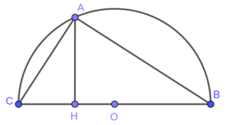
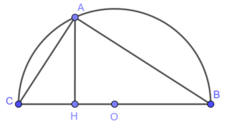
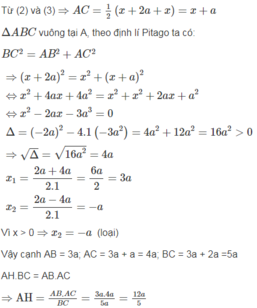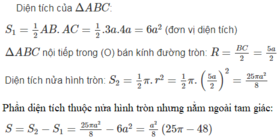Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau :
\(BC=AB+2a\)
\(AC=\dfrac{1}{2}\left(BC+AB\right)\)
a là một độ dài cho trước
a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác
b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác ssos
c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và AC tạo ra