1.A=\(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}}{2}\)
2.B=\(\left(\dfrac{2\sqrt{x+x+1}}{\sqrt{x}+1}\right)\left(1-\dfrac{x-\sqrt{x}}{\sqrt{x}-1}\right):\left(1-\sqrt{x}\right)\)
3.C=\(\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\dfrac{8\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}-x-3}{x-1}-\dfrac{1}{\sqrt{x}-1}\right)\)
Làm chi tiết hộ mình với ak mình đang cần gấp!!!

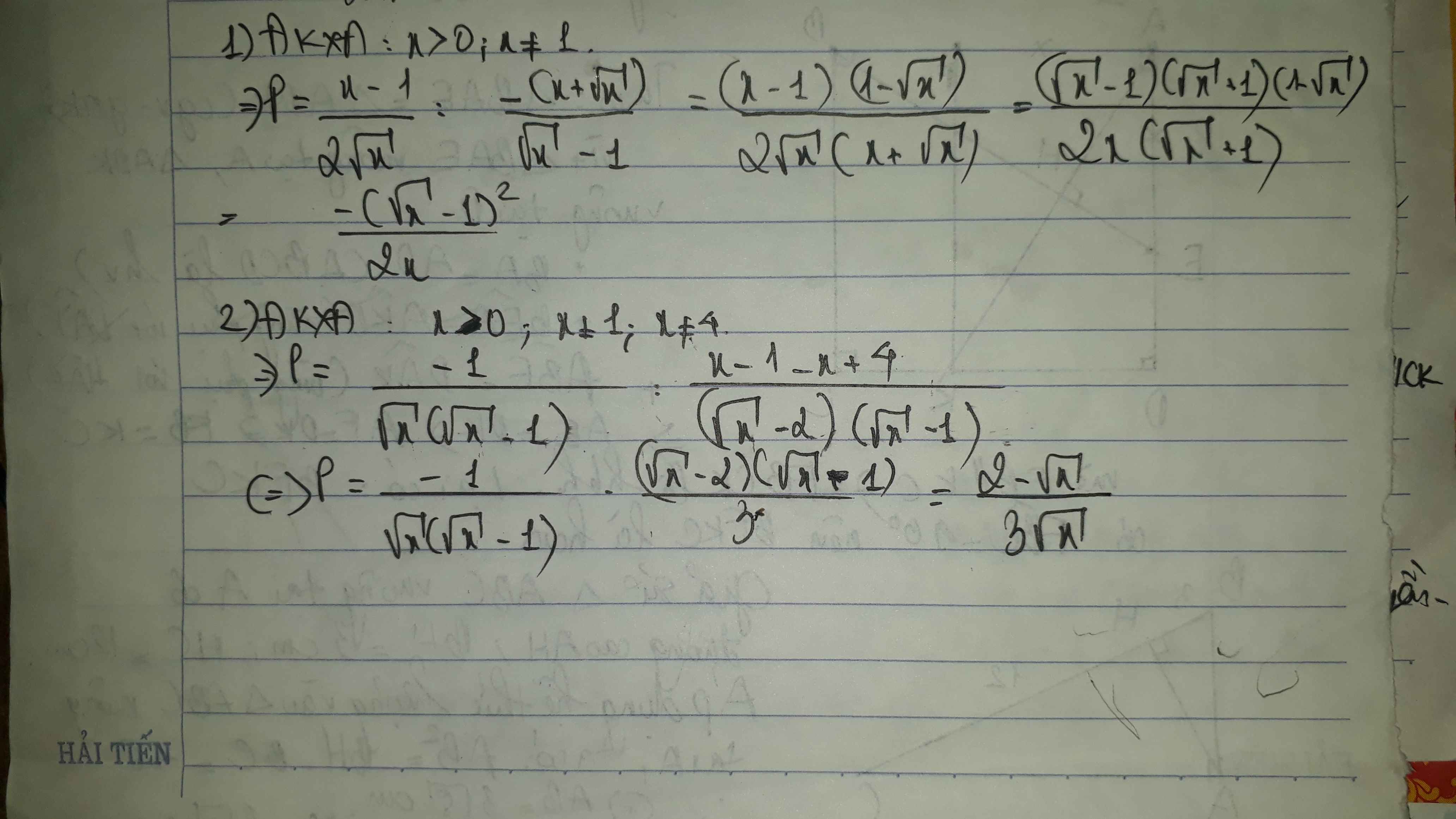
1: Ta có: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}}{2}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-2}{\sqrt{x}\left(x+\sqrt{x}+1\right)}\)