Một đoàn tàu đang chạy với tốc độ 40 km/h thì hãm phanh, chuyển động thẳng chậm dần đều để vào ga. Sau hai phút thì tàu dừng lại ở sân ga.
a) Tính gia tốc của đoàn tàu
b) Tính quãng đường mà tàu đi được trong thời gian hãm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
21 tháng 12 2017
Quãng đường mà tàu đi đi được trong thời gian hãm phanh là:
VT
23 tháng 1 2018
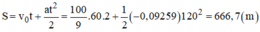
Ta có: Ban đầu v0 = 40 km/h = 100/9 m/s.
Sau đó Δt = 2 phút = 120 s thì tàu dừng lại: v = 0
Gia tốc của đoàn tàu là:
VT
21 tháng 8 2018
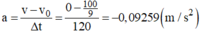
Chọn chiều dương là chiều chuyển động.
a) Gia tốc: a = v − v 0 Δ t = 0 − 12 2 , 5.60 = − 0 , 08 m/s2.
b) Từ v 2 − v 0 2 = 2 a s ⇒ quãng đường tàu đi được trong thời gian hãm:
s = v 2 − v 0 2 2 a = 0 − 12 2 2. ( − 0 , 08 ) = 900 (m).
23 tháng 9 2021
Tóm tắt :
Cđộng : CDĐ
\(v0=43,2km\text{/ }h=12m\text{/ }s\)
v=0
t = 2' =120s
a) a =?
b) s =?
GIẢI :
a) Gia tốc \(a=\dfrac{v-v_0}{t}=\dfrac{0-12}{120}=0,1\left(m\text{/}s^2\right)\)
b) Quãng đường mà tàu đi đc trong thời gian hãm phanh là:
\(s=v_0t+\dfrac{1}{2}at^2=12.120+\dfrac{1}{2}.\left(-0,1\right).120^2=720\left(m\right)\)
7 tháng 10 2021
Đổi 40 km/h = 11 m/s
2 phút= 120s
a) Gia tốc của đoàn tàu là:
\(a=\dfrac{v-v_0}{t}=\dfrac{0-11}{120}=-0,09\left(\dfrac{m}{s^2}\right)\)
b) Quãng đường mà tàu đi được trong thời gian hãm là:
\(s=\dfrac{v^2-v^2_0}{2a}=\dfrac{0^2-11^2}{2\cdot\left(-0,09\right)}=672,2\left(m\right)\)
Chọn gốc tọa độ, gốc thời gian lúc tàu bắt đầu hãm phanh, chiều dương là chiều chuyển động.
Ta có: v0 = 40 km/h =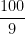
m/s; v = o
t = 2 phút = 120s
a) gia tốc: a =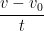
= 
= 
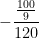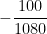
a = - 0,0925 m/s2.
b) Quãng đường tàu đi được: s = v0t +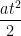
=> s =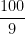
x 120 - 
≈ 667,3m
=> s ≈ 667,3m.
vo=40km/h=100/9 m/s; v=o; t=2'=120s
a=(v-v0)/t=-5/54(m/s2)
S=v0t+(at2)/2=2000/3=666,67(m)