Ba điểm A, B, C phân biệt tạo nên vectơ \(\overrightarrow{AB}+\overrightarrow{AC}\) vuông góc với vectơ \(\overrightarrow{AB}+\overrightarrow{CA}\). Vậy tam giác ABC là tam giác gì ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


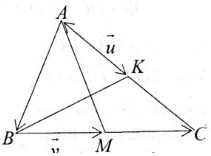
Gọi G là giao điểm của AK, BM thì G là trọng tâm của tam giác.
Ta có 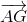 =
= 
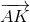 =>
=> 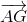 =
=

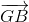 = -
= -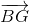 = -
= -
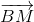 = -
= -

Theo quy tắc 3 điểm đối với tổng vec tơ:
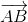 =
= 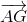 +
+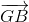 =>
=> 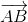 =
= 
 -
- 
 =
=  (
( -
-  ).
).
AK là trung tuyến thuộc cạnh BC nên
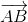 +
+ 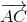 = 2
= 2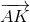 =>
=> 
 -
- 
 +
+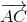 = 2
= 2
Từ đây ta có 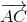 =
= 
 +
+
 =>
=> 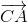 = -
= -
 -
- 
 .
.
BM là trung tuyến thuộc đỉnh B nên
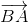 +
+ 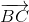 = 2
= 2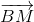 => -
=> - 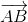 +
+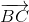 = 2
= 2
=> 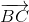 =
= 
 +
+
 .
.

Lời giải:
Theo đề ta có: $\overrightarrow{BM}=2\overrightarrow{MC}=-2\overrightarrow{CM}$
$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}(1)$
$=\overrightarrow{AB}-2\overrightarrow{CM}$
$\overrightarrow{AM}=\overrightarrow{AC}+\overrightarrow{CM}$
$\Rightarrow 2\overrightarrow{AM}=2\overrightarrow{AC}+2\overrightarrow{CM}(2)$
Lấy $(1)+(2)\Rightarrow 3\overrightarrow{AM}=\overrightarrow{AB}+2\overrightarrow{AC}$
$\Rightarrow \overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$

Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
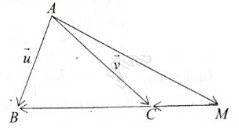
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)


Gọi M là trung điểm của cạnh BC ta có :
\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}=\overrightarrow{AD}\)
Mặt khác :
\(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}\)
Theo giả thiết ta có :
\(\left|2\overrightarrow{AM}\right|=\left|\overrightarrow{CB}\right|=\left|\overrightarrow{AD}\right|\) hay \(AM=\dfrac{BC}{2}\)
Ta suy ra ABC là tam giác vuông tại A
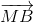 = 3
= 3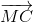 =>
=> 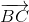 )
)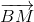 =
= 
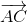 -
- 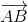 nên
nên 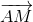 =
= 

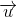 +
+ 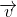
Theo giả thiết ta có :
\(\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AB}+\overrightarrow{CA}\right)=0\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AB}-\overrightarrow{AC}\right)=0\)
\(\Leftrightarrow\overrightarrow{AB}^2-\overrightarrow{AC}^2=0\)
Ta suy ra ABC là tam giác có \(AB=AC\) (Tam giác cân tại A)