Tổng ba phân số tối giản bằng 39/20, tử số của phân số thứ nhấ t,phân số thứ hai, phân số thứ ba tỷ lệ với 3;7;11 v à mẫu của ba phân số đó theo thứ tự tỷ lệ với 10;20;40.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hatsune Miku này ai trả biết là dùng dãy tỉ số cách đều cái mình cần là cách làm

Tổng 3 p/s tối giản là 37/20. biết tử của phân số thứ 1; phân số thứ 2;phân số thứ 3 lần lượt tỉ lệ với 3,7,11. mẫu của 3 phân số đó cũng lần lượt tỉ lệ với 10,20,40. tìm 3 phân số đó.\
Bài làm.

Gọi các phân số cần tìm là x, y, z.
Tổng của ba phân số bằng 1 nên:
x + y + z = 1 (1)
Hiệu của phân số thứ nhất và thứ hai bằng phân số thứ ba nên:
x - y = z (2)
Tổng của phân số thứ nhất và thứ hai bằng 5 lần phân số thứ ba nên:
x + y = 5z (3)
Từ (1), (2), (3) ta có hệ:
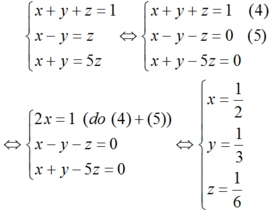
Vậy ba phân số cần tìm lần lượt là:
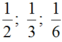
Gọi ba phân số lần lượt cần tìm là: \(\frac{a}{x};\frac{b}{y};\frac{c}{z}\left(x,y,z\ne0\right)\)
Theo bài ra, ta có:
\(\frac{a}{3}=\frac{b}{7}=\frac{c}{11}\)(1)
\(\frac{x}{10}=\frac{y}{20}=\frac{z}{40}\Leftrightarrow x=\frac{y}{2}=\frac{z}{4}\)(2)
Từ (1)(2) =>
\(\frac{\frac{a}{3}}{x}=\frac{\frac{b}{7}}{\frac{y}{2}}=\frac{\frac{c}{11}}{\frac{z}{4}}=\frac{\frac{a}{x}}{3}=\frac{\frac{b}{y}}{\frac{7}{2}}=\frac{\frac{c}{z}}{\frac{11}{4}}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{\frac{a}{x}}{3}=\frac{\frac{b}{y}}{\frac{7}{2}}=\frac{\frac{c}{z}}{\frac{11}{4}}=\frac{\frac{a}{x}+\frac{b}{y}+\frac{c}{z}}{3+\frac{7}{2}+\frac{11}{4}}=\frac{\frac{39}{20}}{\frac{37}{4}}=\frac{39}{185}\)
\(\frac{a}{x}=\frac{39}{185}.3=\frac{117}{185}\)
\(\frac{b}{y}=\frac{39}{185}.\frac{7}{2}=\frac{273}{370}\)
\(\frac{c}{z}=\frac{39}{185}.\frac{11}{4}=\frac{429}{740}\)