10/ tìm x ( áp dụng kiến thức phân tích đa thức thành nhân tử) d,2x^3+3x^2+3+2x =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2021
a: Ta có: \(2-x=2\left(x-2\right)^3\)
\(\Leftrightarrow2\left(x-2\right)^3+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left[2\left(x-2\right)^2+1\right]=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
c: Ta có: \(\left(x-1.5\right)^6+2\left(1.5-x\right)^3=0\)
\(\Leftrightarrow\left(x-1.5\right)^6-2\left(x-1.5\right)^3=0\)
\(\Leftrightarrow\left(x-1.5\right)^3\cdot\left[\left(x-1.5\right)^3-2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1.5\\x=\sqrt[3]{2}+1.5\end{matrix}\right.\)
20 tháng 8 2021
\(\left(x^2+2x\right)^2-2x^2-4x-3=0\Leftrightarrow x^4+4x^3+4x^2-2x^2-4x-3=0\Leftrightarrow x^4+4x^3+2x^2-4x-3=0\Leftrightarrow\left(x-1\right)\left(x+1\right)^2\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=3\end{matrix}\right.\)
20 tháng 8 2021
Ta có: \(\left(x^2+2x\right)^2-2x^2-4x-3=0\)
\(\Leftrightarrow\left(x^2+2x\right)^2-2\left(x^2+2x\right)-3=0\)
\(\Leftrightarrow\left(x^2+2x-3\right)\left(x^2+2x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\cdot\left(x+3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-3\\x=1\end{matrix}\right.\)
12 tháng 8 2021
Ta có: \(\left(x-2\right)^3+\left(5-2x\right)^3=0\)
\(\Leftrightarrow\left(x-2+5-2x\right)\left[\left(x-2\right)^2-\left(x-2\right)\left(5-2x\right)+\left(5-2x\right)^2\right]=0\)
\(\Leftrightarrow3-x=0\)
hay x=3
19 tháng 8 2021
a) \(x^3+3x^2+3x=0\Rightarrow x\left(x^2+3x+3\right)=0\Rightarrow x\left[\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}\right]=0\Rightarrow x=0\)
(do \(\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\))
b) \(x^3+6x^2+12x=0\Rightarrow x\left(x^2+6x+12\right)=0\Rightarrow x\left[\left(x+3\right)^2+4\right]=0\Rightarrow x=0\)
(do (x+3)2+4≥4>0)
19 tháng 8 2021
a: Ta có: \(x^3+3x^2+3x=0\)
\(\Leftrightarrow x\left(x^2+3x+3\right)=0\)
hay x=0
b: Ta có: \(x^3+6x^2+12x=0\)
\(\Leftrightarrow x\left(x^2+6x+12\right)=0\)
hay x=0
11 tháng 8 2021
Bn ơi bn có thể giải thích câu đầu tiên đoạn sau giấu <=> đc ko?
TB
3
NT
28 tháng 10 2016
Ta có
2x^4-x^3+2x^2+3x-2
=x^3(2x-1)+(2x^2-x)+(4x-2)
=x^3(2x-1)+x(2x-1)+2(2x-1)
=(x^3+x+2)(2x-1)
4 tháng 1 2022
Bài 1:
a: \(=6x^3-10x^2+6x\)
b: \(=-2x^3-10x^2-6x\)
Bài 4:
a: =>3x+10-2x=0
=>x=-10
c: =>3x2-3x2+6x=36
=>6x=36
hay x=6
4 tháng 1 2022
Bài 1:
\(a,=6x^3-10x^2+6x\\ b,=-2x^3-10x^2-6x\)
Bài 4:
\(a,\Leftrightarrow3x+10-2x=0\Leftrightarrow x=-10\\ b,\Leftrightarrow x\left(2x^2+9x-5\right)-\left(2x^3+9x^2+x+4,5\right)=3,5\\ \Leftrightarrow2x^3+9x^2-5x-2x^3-9x^2-x-4,5=3,5\\ \Leftrightarrow-6x=8\Leftrightarrow x=-\dfrac{4}{3}\\ c,\Leftrightarrow3x^2-3x^2+6x=36\Leftrightarrow x=6\)
Bài 1:
\(a,=7xy\left(2x-3y+4xy\right)\\ b,=x\left(x+y\right)-5\left(x+y\right)=\left(x-5\right)\left(x+y\right)\\ c,=\left(x-y\right)\left(10x+8\right)=2\left(5x+4\right)\left(x-y\right)\\ d,=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\\ =2x\left(4x+2\right)=4x\left(2x+1\right)\\ e,=5\left[\left(x-y\right)^2-4z^2\right]=5\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=x^2+8x-x-8=\left(x+8\right)\left(x-1\right)\\ g,\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\\ h,=x^2+3x+x+3=\left(x+3\right)\left(x+1\right)\)
DT
3
22 tháng 12 2021
\(a,=5x^2-5x+3x-3=\left(x-1\right)\left(5x+3\right)\\ b,=2x^2-5x+2x-5=\left(2x-5\right)\left(x+1\right)\\ c,=x^2+5x-3x-15=\left(x+5\right)\left(x-3\right)\\ d,=7x^2-7x+x-1=\left(x-1\right)\left(7x+1\right)\)
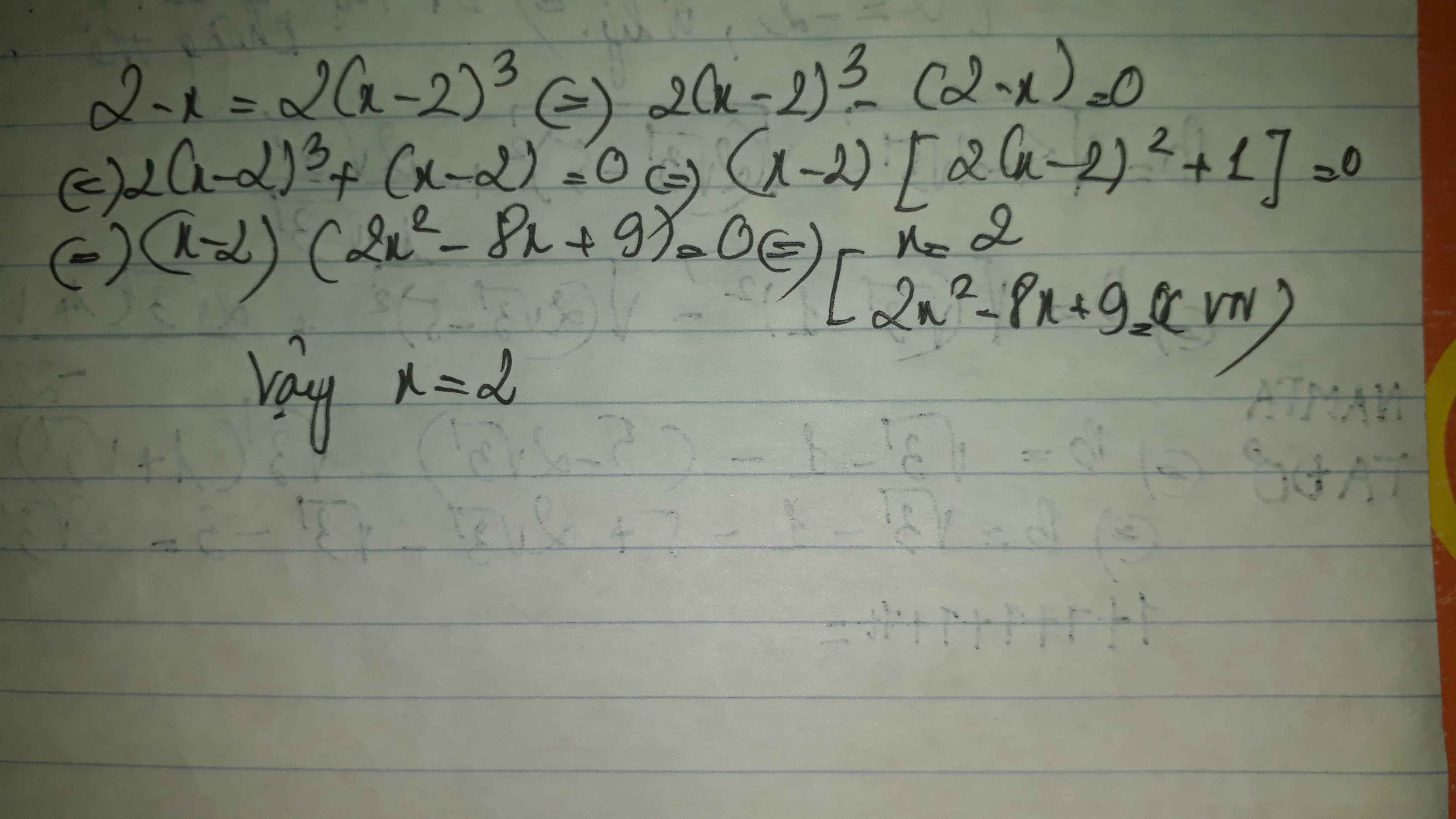
Ta có: \(2x^3+3x^2+2x+3=0\)
\(\Leftrightarrow x^2\left(2x+3\right)+\left(2x+3\right)=0\)
\(\Leftrightarrow2x+3=0\)
hay \(x=-\dfrac{3}{2}\)