
 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


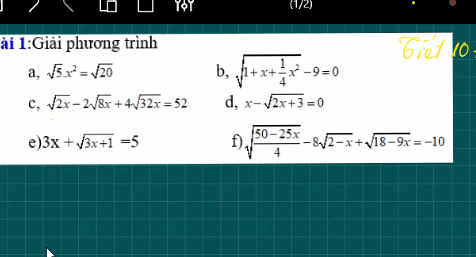
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14


a) Xét ΔABC vuông tại A và ΔFEC vuông tại F có
\(\widehat{ECF}\) chung
Do đó: ΔABC\(\sim\)ΔFEC(g-g)
Suy ra: \(\dfrac{CA}{CF}=\dfrac{CB}{CE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(CA\cdot CE=CB\cdot CF\)(Đpcm)
b) Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)


16)
a) Tam giác ABC vuông tại A : \(AB^2+AC^2=BC^2\)
BC=10 ⇒FC=10-5.2=4.8
b) Tam giác ABC và tam giác FEC có
C chung
\(\dfrac{AC}{FC}=\dfrac{BC}{EC}=0.6\)
Do đó tam giác ABC đồng dạng với tam giác FEC (C-G-C)
c)⇒Góc FEC=ABC=AEM
Tam giác MAE và tam giác MFB có
Góc M chung
Góc AEM = MBF (CMT)
⇒ 2 Tam giác đồng dạng (G-G)
⇒\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)⇒ MA.MB=MF.MB
a) Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) (Định lí Py-ta-go)
=> \(BC^2=6^2+8^2=100\)
=> BC = 10 (cm)
=> CF = BC\(-\)BF = 10 - 5,2 = 4,8 (cm)
Vậy BC = 10 cm ; CF = 4,8 cm
b) Xét \(\Delta CAB\) và \(\Delta CFE\) có
\(\left\{{}\begin{matrix}\widehat{C}:chung\\\dfrac{CF}{CE}=\dfrac{CA}{CB}\left(\dfrac{4,8}{6}=\dfrac{8}{10}=\dfrac{4}{5}\right)\end{matrix}\right.\)
=>\(\Delta CAB\sim\Delta CFE\) (c-g-c)
Vậy \(\Delta CAB\sim\Delta CFE\)
c) Xét \(\Delta MAEvà\Delta MFB\) có
\(\left\{{}\begin{matrix}\widehat{M}:chung\\\widehat{MAE}=\widehat{MFB}=90^0\end{matrix}\right.\)
=> \(\Delta MAE\sim\Delta MFB\) (g-g)
=> \(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=> MA.MB = MF.ME
Vậy MA.MB = ME.MF
d) Xét \(\Delta BMF\) và \(\Delta BCA\) có
\(\left\{{}\begin{matrix}\widehat{B}:chung\\\widehat{BFM}=\widehat{BAC}=90^0\end{matrix}\right.\)
=> \(\Delta BMF\) \(\sim\)\(\Delta BCA\) (g-g)
=> \(\dfrac{MF}{AC}=\dfrac{BF}{BA}\)
=> MF = \(\dfrac{8.5,2}{6}\) = \(\dfrac{104}{15}\approx6,9\left(cm\right)\)
Vậy MF \(\approx6,9\left(cm\right)\)

ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm

Bài 2:
Gọi K là trung điểm của AD và O là trung điểm của BC
Xét ΔABC có
P là trung điểm của AC
O là trung điểm của BC
Do đó: PO là đường trung bình của ΔABC
Suy ra: PO//AB
hay PO//CD
Xét ΔDAB có
K là trung điểm của AD
Q là trung điểm của BD
Do đó: KQ là đường trung bình của ΔDAB
Suy ra: KQ//AB
hay KQ//CD
Xét ΔBDC có
Q là trung điểm của BD
O là trung điểm của BC
Do đó: QO là đường trung bình của ΔBDC
Suy ra: QO//DC
Ta có: QO//DC
mà PO//DC
và QO,PO có điểm chung là O
nên Q,P,O thẳng hàng
Ta có: KQ//CD
QO//CD
mà KQ và QO có điểm chung là Q
nên K,Q,O thẳng hàng
mà Q,P,O thẳng hàng
nên K,Q,P,O thẳng hàng
hay QP//DC(1)
Xét ΔEAB có
M là trung điểm của EA
N là trung điểm của EB
Do đó: MN là đường trung bình của ΔEAB
Suy ra: MN//AB
hay MN//DC(2)
Từ (1) và (2) suy ra MN//PQ
Xét tứ giác MNPQ có MN//PQ
nên MNPQ là hình thang








MNE = MPF
MND =MPD
DME = DMF
3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau