Cho hàm số y=x4−5x2+4 có đồ thị (C). Biết rằng mo là giá trị của tham số m để đường thẳng d:y=m cắt đồ thị (C) tại 4 điểm phân biệt cách đều nhau. Giá trị của mo thuộc khoảng nào sau đây?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 8 2017
Đáp án C
Đồ thị hàm số y = x 3 - 3 x + 1 là đồ thị bên dưới
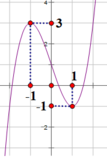
Từ đồ thị hàm số y = x 3 - 3 x + 1 suy ra đồ thị hàm số y = x 3 - 3 x + 1 là đồ thị bên dưới
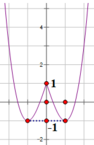
Dựa vào đồ thị hàm số y = x 3 - 3 x + 1 và đồ thị hàm số y = 2 m - 1
Ta có: đường thẳng y = 2 m - 1 cắt đồ thị hàm số y = x 3 - 3 x + 1 tại 4 điểm phân biệt
⇔ - 1 < 2 m - 1 < 1 ⇔ 0 < m < 1
CM
12 tháng 10 2019
Đáp án B
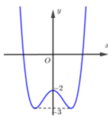
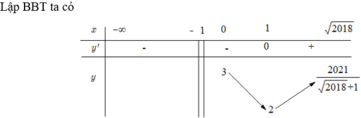
Dựa vào đồ thị hàm số y = x 4 − 2 x 2 − 2
Suy ra − 3 < m < − 2 là giá trị cần tì
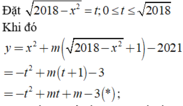
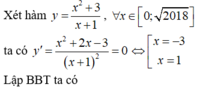
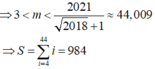
Phương trình hoành độ giao điểm: \(x^4-5x^2-m+4=0\)
Đặt \(x^2=t\Rightarrow t^2-5t-m+4=0\) (1)
Gọi 4 hoành độ giao điểm là \(x_1< x_2< x_3< x_4\) và \(t_1< t_2\) là 2 nghiệm dương phân biệt của (1) thì: \(\left\{{}\begin{matrix}x_1=-\sqrt{t_2}\\x_2=-\sqrt{t_1}\\x_3=\sqrt{t_1}\\x_4=-\sqrt{t_2}\end{matrix}\right.\)
Do 4 điểm cách đều \(\Rightarrow x_2-x_1=x_3-x_2\Rightarrow x_1+x_3=2x_2\)
\(\Rightarrow-\sqrt{t_2}+\sqrt{t_1}=-2\sqrt{t_1}\) \(\Rightarrow3\sqrt{t_1}=\sqrt{t_2}\Rightarrow t_2=9t_1\)
\(\Rightarrow\left\{{}\begin{matrix}t_1+t_2=5\\t_2=9t_1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}t_1=\dfrac{1}{2}\\t_2=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow-m+4=t_1t_2=\dfrac{9}{4}\)
\(\Rightarrow m=\dfrac{7}{4}\)