Question

[Nguyễn Thị Ngọc Bảo]

1. Cho tam giác ABC có góc A bằng 90 độva AB=AC .Qua A kẻ đường thẳng d sao cho BC nằm cùng phía đối với d .Kẻ BD và CE vuông góc với d(DE thuộc d)

Chứng minh rằng BD=AEvà AD=CE

2. Cho tam giác ABC nhọn . Gọi M là trung điểm của cạnh AC . Trên tia đối MB lấy D sao cho MD=MB.

a.Chứng minh :t/g ABM=t/g CDM

b. Chứng minh :AD//BC

c. Gọi N là trung điểm của BC đường thẳng NM cắt AD tại E Chứng minh M là trung điểm của NE

Giups minh nhé các bạn!

Answer 1

[Hoàng Thị Ngọc Anh]

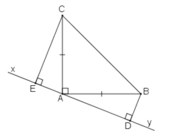
Câu 1:

Vì BD \(\perp\) d nên \(\widehat{BDA}\) = 90^o

Ta có:

\(\widehat{BAD}\) + \(\widehat{BAC}\) + \(\widehat{CAE}\) = 180^o

=> \(\widehat{BAD}\) + 90^o + \(\widehat{CAE}\) = 180^o

=> \(\widehat{BAD}\) + \(\widehat{CAE}\) = 90^o (1)

Áp dụng tính chất tam giác vuông ta có:

\(\widehat{DBA}\) + \(\widehat{BAD}\) = 90^o (2)

Từ (1) và (2) suy ra:

\(\widehat{BAD}\) + \(\widehat{CAE}\) = \(\widehat{DBA}\) + \(\widehat{BAD}\)

=> \(\widehat{CAE}\) = \(\widehat{DBA}\)

Xét \(\Delta\)DBA vuông tại D và \(\Delta\)EAC vuông tại E có:

BA = AC (giả thiết)

\(\widehat{DBA}\) = \(\widehat{EAC}\) (chứng minh trên)

=> \(\Delta\)DBA = \(\Delta\)EAC (cạnh huyền - góc nhọn)

=> DB = EA và DA = EC (2 cặp cạnh tương ứng).

Câu 2: Mk sẽ làm ở đây: /hoidap/question/166568.html