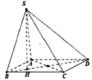
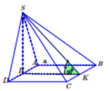
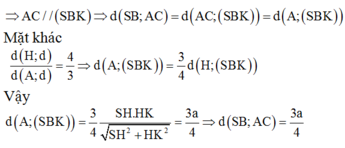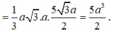Cho hình chóp SABCD đáy ABCD là hình chữ nhật tâm I ,AB =a, BC=a căn 3 .Tam giác SIA cân tại S . (SAD) vuông góc với đáy .góc giữa SD và (ABCD) = 60* .Tính thể tích khối chóp SABCI?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
22 tháng 6 2021
Lời giải:
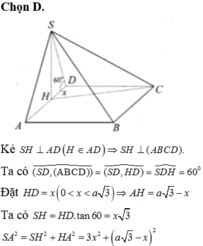
Lấy $H$ là trung điểm $AB$ thì do $SAB$ cân tại $S$ nên $SH\perp BH$
$BH$ là giao tuyến của $(SAB), (ABCD)$; (SAB)\perp (ABCD)$ nên $SH\perp (ABCD)$
$\Rightarrow (SC, (ABCD))=(SC, CH)=\widehat{SCH}=45^0$
$\Rightarrow SH=CH=\sqrt{BC^2+BH^2}=\sqrt{(2a)^2+(\frac{a}{2})^2}=\frac{\sqrt{17}}{2}a$
\(V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{17}}{2}a.a.2a=\frac{\sqrt{17}}{3}a^3\)
CM
17 tháng 2 2019
Đáp án D.
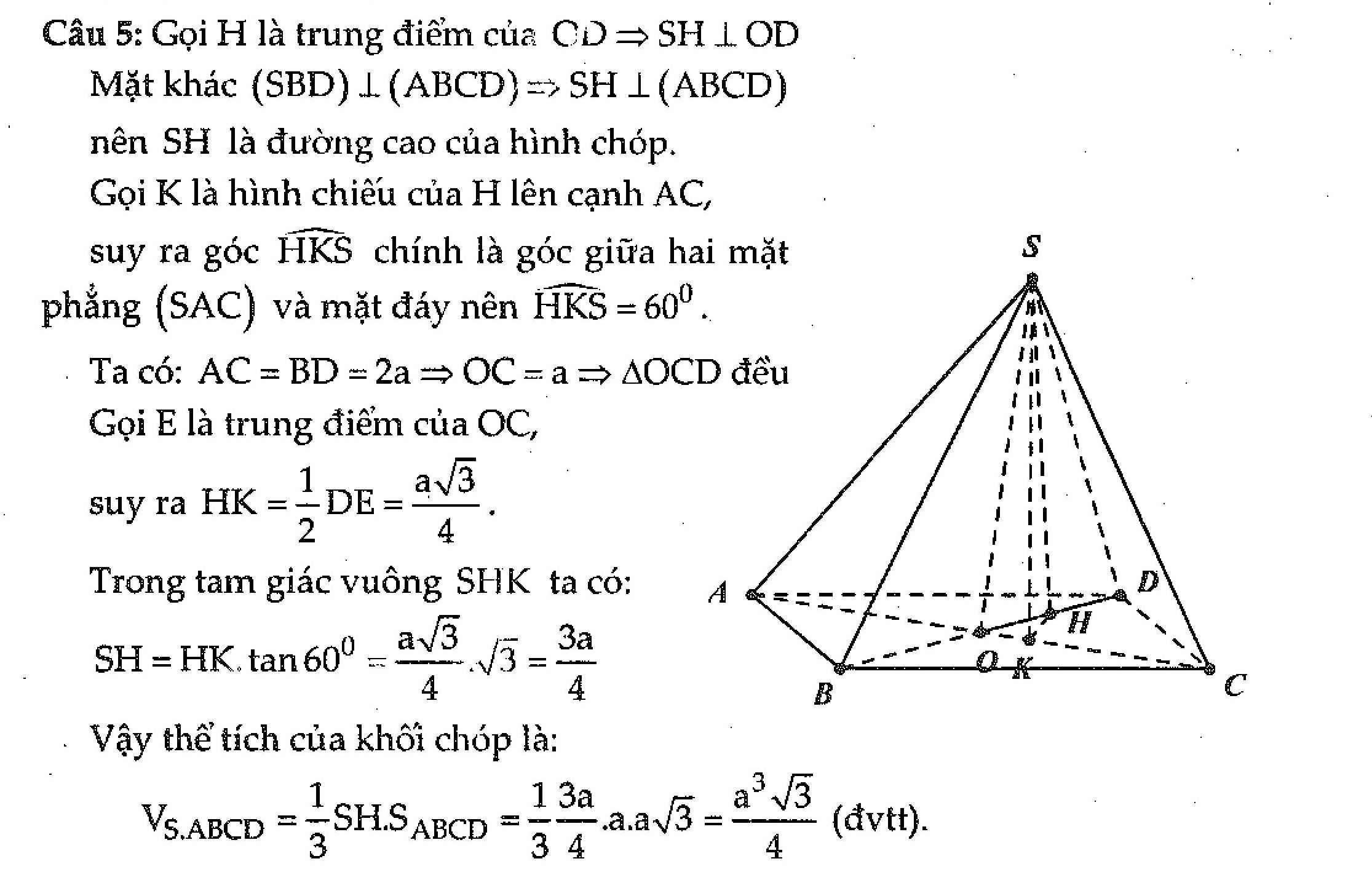
Hướng dẫn giải:
Kẻ S H ⊥ A B ⇒ S H ⊥ ( A B C D )
Do ∆ S B D vuông tại S nên H B H D = S B S D 2 = 1 3
Ta có B D = A B 2 + A D 2 = a 7
⇒ H D = 3 a 7 4
Mặt khác
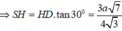
Ta có S A B C D = A B . A D = 2 a 3 2
V S . A B C D = 1 3 S H . S A B C D = a 7 2 2
