Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
D là TĐ của AB mà DE //BC nên DE là đg TB của tam giác ABC -->E là TĐ của AC.
E là TĐ của AC mà EF //AB nên EF là đg TB của tam giác CAB--->F là TĐ của BC
a: ΔCEF đồng dạng với ΔCAB theo tỉ số k=CE/CA
ΔADE đồng dạng với ΔABC
=>k'=AD/AB=2/5
b: \(\dfrac{C_{ADE}}{C_{ABC}}=\dfrac{AD}{AB}=\dfrac{2}{5}\)
=>\(C_{ADE}=\dfrac{2}{5}\cdot\left(5+7+9\right)=\dfrac{2}{5}\cdot21=\dfrac{42}{5}\left(cm\right)\)
ΔCEF đồng dạng với ΔCAB
=>\(\dfrac{C_{CEF}}{C_{CAB}}=\dfrac{CE}{CA}=\dfrac{3}{5}\)
=>\(C_{CEF}=\dfrac{3}{5}\cdot\left(5+7+9\right)=\dfrac{3}{5}\cdot21=\dfrac{63}{5}\left(cm\right)\)
+)Xét tam giác BDF và ∆EFD có:
DF chung
∠BDF = ∠DFE ( hai góc so le trong; BC// EF)
∠BFD = ∠FDE ( hai góc so le trong; DE// AB)
Suy ra:∆ BDF = ∆EFD (g.c.g)
Suy ra BD = EF. Theo giả thiết, D là trung điểm của BC nên CD = DB = EF.
+) Xét ∆ CDE và ∆ EFA có :
CD = EF ( chứng minh trên)
∠(CDE) = ∠(EFA) = ∠(CBA)
∠(ECD) = ∠(AEF) (các góc đồng vị).
Suy ra: ∆ CDE = ∆ EFA ( g.c.g)
Suy ra CE = EA nên E là trung điểm của CD.
Xét ΔODE và ΔOCB có
góc ODE=góc OCB
góc DOE=góc COB
=>ΔODE đồng dạng với ΔOCB
=>OD/OC=OE/OB
=>OD*OB=OC*OE
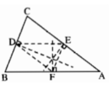
Theo đề đúng thì lm như sau:
a) Có: DE // BF (gt)
EF // BD (gt)
Suy ra BD = EF (theo tính chất đoạn chắn) (đpcm)
b) Vì EF // AB (gt) => ADE = DEF (so le trong) (1)
ED // BC (gt) => DEF = EFC (so le trong) (2)
Từ (1) và (2) => ADE = EFC
Xét t/g ADE và t/g EFC có:
EAD = CEF ( đồng vị)
AD = EF ( cùng = BD)
ADE = EFC (cmt)
Do đó, t/g ADE = t/g EFC (g.c.g) (đpcm)
c) Xét t/g MFE và t/g MDB có:
MF = MD (gt)
MFE = MDB (so le trong)
FE = DB (câu a)
Do đó, t/g MFE = t/g MDB (c.g.c)
=> EMF = BMD (2 góc tương ứng)
Mà EMF + EMD = 180o
Nên BMD + EMD = 180o
=> BME = 180o
hay B,M,E thẳng hàng (đpcm)
Đề sai rồi Trang ơi, xem lại đi