bài 1: Cho tam giác ABC gọi D là điểm nằm giữa B và C, qua D vẽ DE // BC và DF // ACa/ chứng minh tứ giác AEDF là hình bình hành.b/ Khi nào thì hình bình hành AEDF là hình thoi, hình vuông.bài 2: cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm AC, K đối xứng với M qua I.a/ chứng minh AMCK là hình chữ nhật.b/ điều kiện của tam giác ABC để AMCK là hình vuông.bài 3: Cho hình thoi ABCD, O là giao điểm...
Đọc tiếp
bài 1: Cho tam giác ABC gọi D là điểm nằm giữa B và C, qua D vẽ DE // BC và DF // AC
a/ chứng minh tứ giác AEDF là hình bình hành.
b/ Khi nào thì hình bình hành AEDF là hình thoi, hình vuông.
bài 2: cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm AC, K đối xứng với M qua I.
a/ chứng minh AMCK là hình chữ nhật.
b/ điều kiện của tam giác ABC để AMCK là hình vuông.
bài 3: Cho hình thoi ABCD, O là giao điểm hai đường chéo. Qua B vẽ đường thẳng song song với AC, qua C vẽ đường thẳng song song với BD, hai đường thẳng đó cắt nhau tại K.
a/ chứng kinh OBKC là hình vuông.
b/ chứng minh AB = OK.
c/ điều kiện của tứ giác ABCD để OBKC là hình vuông.
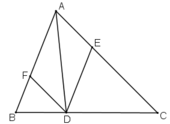
```````````` Giúp mk phần b bài 1 và bài 2, phần c bài 3 `````````````````
Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A