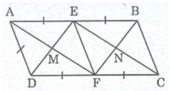
Cho hình bình hành ABCD có AB=2AD. Gọi E,F lần lượt là trung điểm của AB và CD.
a) Chứng minh BEDF là hình bình hành
b) Chúng minh AF vuông góc DE
c) Gọi M là giao điểm của AF và DE, N là giao điểm của EC và BF. Chứng minh MN=EF
d) Hãy bổ sung thêm điều kiện vào đề bài để tứ giác EMNF là hình vuông
( vẽ hình cho mình xem luôn nha, mong mb giúp mình làm bài này) :)))

a: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
b: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi
=>DE vuông góc với AF
Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
mà BC=BE
nên BEFC là hình thoi
=>EC vuông góc với BF
Xét ΔEDC có
EF là đường trung tuyến
EF=DC/2
Do đó: ΔEDC vuông tại E
Xét tứ giác EMFN có \(\widehat{EMF}=\widehat{ENF}=\widehat{MEN}=90^0\)
nên EMFN là hình chữ nhật
Suy ra: EF=MN