Bai 1 :
CHO HBH ABCD ĐG PHÂN GIÁC CỦA GÓC A VÀ GOC C CẮT BD TẠI E VÀ F . CMR 2 HÌNH ABCFE VÀ ADCFE CÓ CÙNG DIỆN TÍCH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 12 2017
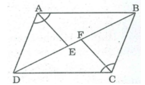
Ta có:
△ ABE = △ CDF (g.c.g) ⇒ S A B E = S C D F (l)
△ AED = △ CFB (g.c.g) ⇒ S A E D = S C F B (2)
Từ (1) và (2) ⇒ S A B E + S C F B = S C D F + S A E D
Hay S A B C F E = S A D C F E
12 tháng 2 2019
Trên EM lấy trung điểm I.Kẻ IH vuông vs DC.
IH là đg trug bình của hình thang EDCM
=> DH=HC
mà DF=KC
Trừ theo vế đc :FH=HK
Tam giác IFH có: IH là đg cao,là trung tuyến
\Rightarrowtam giác IFH cân $\Rightarrow IF = IK = \frac{{EM}}{2}$
=> Tam giac EFM vuông hay $\widehat {EFM} = {90^0}$
12 tháng 6 2017
Ta có: góc A+B+C+D=360 =>C+D=150 độ
Tính góc CED + EDC=1/2C+1/2D=1/2(C+D)=75(do phân giác)
=>E=180-75=105
ta có góc tạo bởi 2 tia phân giác của 2 góc kề có tổng là 90 độ (có cm trong sgk)
nên ECF+EDF=90+80=180 độ
=>CFD= 360-180-105=75
Xong rồi, nhưng bạn lập luận chặt chẽ hơn nhé
