Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔABH,ΔAKHΔABH,ΔAKH có:
BH=HK(gt)BH=HK(gt)
ˆAHB=ˆAHKAHB^=AHK^
AH: cạnh chung
⇒ΔABH=ΔAKH(c−g−c)⇒ΔABH=ΔAKH(c−g−c)
b) Vì ΔABH=ΔAKHΔABH=ΔAKH
⇒AB=AK⇒AB=AK ( cạnh tương ứng ) (1)
Xét ΔAMK,ΔCMEΔAMK,ΔCME có:
AM=MC(=12AC)AM=MC(=12AC)
ˆM1=ˆM2M1^=M2^ ( đối đỉnh )
EM=KM(gt)EM=KM(gt)
⇒ΔAMK=ΔCME(c−g−c)⇒ΔAMK=ΔCME(c−g−c)
⇒EC=AK⇒EC=AK ( cạnh tương ứng ) (2)
Từ (1) và (2) ⇒EC=AB(=AK)⇒EC=AB(=AK)
c) Xét ΔAMEΔAME và ΔCMKΔCMK có:
AM=MC(=12AC)AM=MC(=12AC)
ˆM3=ˆM4M3^=M4^ ( đối đỉnh )
KM=EM(gt)KM=EM(gt)
⇒ΔAME=ΔCMK(c−g−c)⇒ΔAME=ΔCMK(c−g−c)
⇒ˆE1=ˆK1⇒E1^=K1^ ( góc tương ứng )
Mà ˆE1E1^ và ˆK1K1^ ở vị trí so le trong nên AE // KC hay AE // BC
Vậy a) ΔABH=ΔAKH
Hình tự vẽ nhé !
Giải
a) Xét tam giác MHB và tam giác MKC có
MB = MC ( vì M là trung điểm của BC )
HMB = KMC ( vì đối đỉnh )
MH = MK ( vì m là trung điểm của HK )
Do đó Tam giác MHB = tam giác MKC
a) Xét ΔABH vuông tại H và ΔKIH vuông tại H có
HB=HI(gt)
HA=HK(gt)
Do đó: ΔABH=ΔKIH(Hai cạnh góc vuông)
Làm tiếp nha:
Xét tứ giác ABEC có 2 đường chéo AE và BC cắt nhau tại trung điểm M của mỗi đường nên ABEC là hình bình hành.
=> \(\hept{\begin{cases}AB=CE\left(1\right)\\ABllCE\end{cases}}\)
a ) xét \(\Delta ABM\)và \(\Delta ECM\)có:
\(\hept{\begin{cases}MA=ME\left(gt\right)\\MB=MC\left(gt\right)\\AB=CE\left(cmt\right)\end{cases}}\)
---> \(\Delta ABM=\Delta ECM\left(c.c.c\right)\)
b) Xét \(\Delta ABD\) có BH là đường cao đồng thời đường trung tuyến nên \(\Delta ABD\) cân tại B.
---> BC là phân giác của ABD
\(\Delta ABD\)cân tại B ---> AB = BD (2)
Từ (1),(2) ---> BD = CE
Xét tứ giác ABEC có 2 đường chéo AE và BC cắt nhau tại trung điểm M của mỗi đường nên ABEC là hình bình hành
\(\Rightarrow\begin{cases}AB=CE\left(1\right)\\AB\backslash\backslash CE\end{cases}\)
a,xét ΔABM và ΔECM có:
\(\begin{cases}MA=ME\left(gt\right)\\MB=MC\left(gt\right)\\AB=CE\left(cmt\right)\end{cases}\)
→ΔABM=ΔECM(c.c.c)
b,Xét ΔABD có BH là đường cao đồng thời là đường trung tuyến
nên ΔABD cân tại B
→BC là phân giác của \(\widehat{ABD}\)
ΔABD cân tại B →AB=BD(2)
Từ (1),(2)→BD=CE
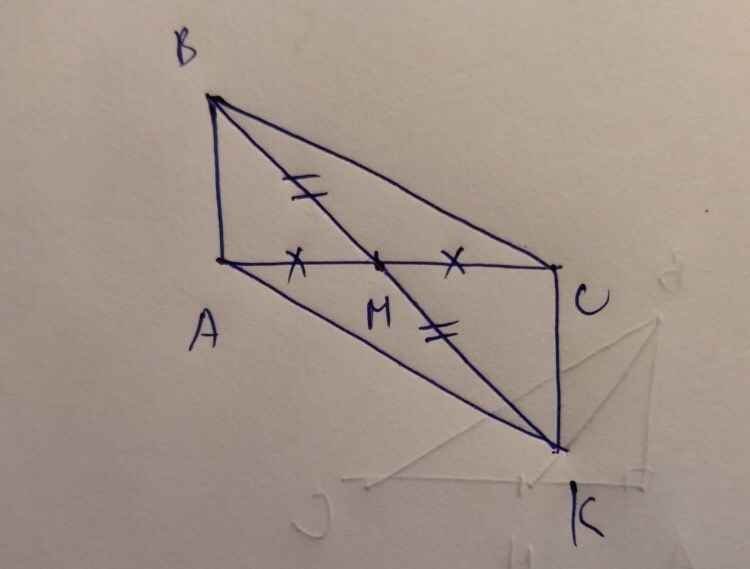
Ta có hình vẽ:
a) Xét Δ ABH và Δ AKH có:
BH = KH (gt)
AHB = AHK = 90o
AH là cạnh chung
Do đó, Δ ABH = Δ AKH (c.g.c) (đpcm)
b) Xét Δ AMK và Δ CME có:
MK = ME (gt)
AMK = CME (đối đỉnh)
AM = CM (gt)
Do đó, Δ AMK = Δ CME (c.g.c)
=> AK = EC (2 cạnh tương ứng) (1)
Δ ABH = Δ AKH (câu a)
=> AB = AK (2 cạnh tương ứng) (2)
Từ (1) và (2) => EC = AB (đpcm)
c) Xét Δ AME và Δ CMK có:
AM = CM (gt)
AME = CMK (đối đỉnh)
ME = MK (gt)
Do đó Δ AME = Δ CMK (c.g.c)
=> AEM = CKM (2 góc tương ứng)
Mà AEM và CKM là 2 góc so le trong nên AE // KC hay AE // BC (đpcm)
Giải:
a) Xét \(\Delta ABH,\Delta AKH\) có:
\(BH=HK\left(gt\right)\)
\(\widehat{AHB}=\widehat{AHK}\)
AH: cạnh chung
\(\Rightarrow\Delta ABH=\Delta AKH\left(c-g-c\right)\)
b) Vì \(\Delta ABH=\Delta AKH\)
\(\Rightarrow AB=AK\) ( cạnh tương ứng ) (1)
Xét \(\Delta AMK,\Delta CME\) có:
\(AM=MC\left(=\frac{1}{2}AC\right)\)
\(\widehat{M_1}=\widehat{M_2}\) ( đối đỉnh )
\(EM=KM\left(gt\right)\)
\(\Rightarrow\Delta AMK=\Delta CME\left(c-g-c\right)\)
\(\Rightarrow EC=AK\) ( cạnh tương ứng ) (2)
Từ (1) và (2) \(\Rightarrow EC=AB\left(=AK\right)\)
c) Xét \(\Delta AME\) và \(\Delta CMK\) có:
\(AM=MC\left(=\frac{1}{2}AC\right)\)
\(\widehat{M_3}=\widehat{M_4}\) ( đối đỉnh )
\(KM=EM\left(gt\right)\)
\(\Rightarrow\Delta AME=\Delta CMK\left(c-g-c\right)\)
\(\Rightarrow\widehat{E_1}=\widehat{K_1}\) ( góc tương ứng )
Mà \(\widehat{E_1}\) và \(\widehat{K_1}\) ở vị trí so le trong nên AE // KC hay AE // BC
Vậy a) \(\Delta ABH=\Delta AKH\)
b) EC = AB
c) AE // BC