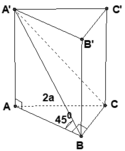
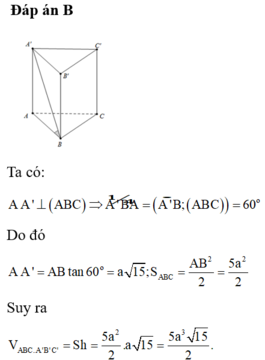
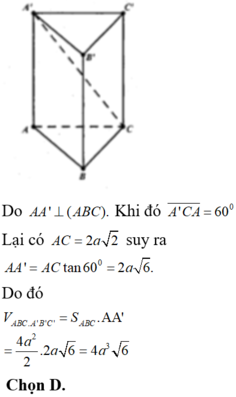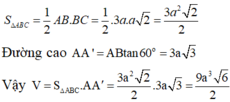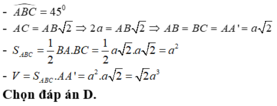Tính thể tích lăng trụ đứng ABC.A'B'C' cân tại a có đáy ABC là tam giác vuông cân tại A ,BC =a√2 , C'B hợp với đáy một góc 60°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
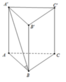
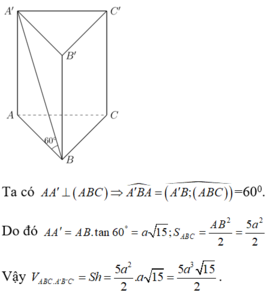
Ta có: A A ' ⊥ A B C ⇒ A ' B A ⏜ = A ' B ; A B C ^ = 60 ∘
Do đó A A ' = A B tan 60 ∘ = a 15 ; S A B C = A B 2 2 = 5 a 2 2
Suy ra V A B C . A ' B ' C ' = S h = 5 a 2 2 . a 15 = 5 a 3 15 2 .

a) Với hình lăng trụ đứng ABC.ABC, diện tích tứ giác ABBA bằng 2a^2 và đáy ABC là tam giác vuông cân tại A, ABa. Thể tích khối lăng trụ ABC.ABC có thể tính bằng công thức: \(V = \frac{1}{3} \times \text{Diện tích đáy} \times \text{Chiều cao}\). Vì đáy ABC là tam giác vuông cân nên diện tích đáy là \(\frac{1}{2} \times a \times a = \frac{1}{2}a^2\). Chiều cao của lăng trụ chính là cạnh AB, vì tam giác ABa là tam giác vuông cân nên \(AB = \sqrt{2}a\). Do đó, thể tích khối lăng trụ ABC.ABC là: \(V = \frac{1}{3} \times \frac{1}{2}a^2 \times \sqrt{2}a = \frac{\sqrt{2}}{6}a^3\). b) Với hình lăng trụ đứng ABC.ABC, góc giữa (ABC) và (ABC) bằng 60°, ta cũng áp dụng công thức tính thể tích khối lăng trụ: \(V = \frac{1}{3} \times \text{Diện tích đáy} \times \text{Chiều cao}\). Diện tích đáy và chiều cao đã được tính tương tự như phần a), ta có thể tính được thể tích khối lăng trụ ABC.ABC.

Chọn A.
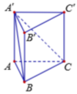
Do đáy tam giác vuông cân tại B, AC = a 2 nên AB = a.
Lại có: ![]() nên góc tạo bởi (A'BC) và đáy là
A
'
B
A
^
nên góc tạo bởi (A'BC) và đáy là
A
'
B
A
^
Theo bài ra: A ' B A ^ = 60 °
![]()
Thể tích V của khối lăng trụ: ![]()