Cho đoạn thẳng AB=4 cm. Vẽ đường tròn tâm A bán kính 2 cm và đường tròn tâm B bán kính 3 cm, chúng cắt nhau ở C và D. C/m rằng AB là tia p/g của góc CAD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
29 tháng 11 2018
Xét \(\Delta\) ACB và\(\Delta\) ADB
Ta có: AC=AD ( bán kính(A)
CB=AD (bán kính(B)
AB là cạch chung
\(\Rightarrow\) \(\Delta\) ACB=\(\Delta\) ADB( c-c-c)
Vậy góc CAB= góc DAB( hai góc tương ứng)
\(\Rightarrow\) AB là tia phân giác của góc CAD
L
5 tháng 11 2019
Tự vẽ hình >:
Nối BC, nối BD
Xét ΔACB và ΔADB có:
AC=AD vì C, D thuộc (A; 3cm)
AB: canh chung
BD=BC vì C, D thuộc (B; 4cm)
=>ΔACB=ΔADB(c.c.c)
=>^CAB=^BAD(hai góc tương ứng)
=>AB là pg ^CAD(đpcm)
5 tháng 11 2019
AC=AD vì C, D thuộc (A;3cm) với
BD=BC vì C,D thuộc (B;4cm) là sao z bn
Còn đpcm là gì
CM
10 tháng 8 2018
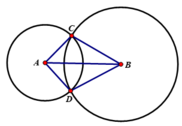
Nối BC, BD, AC, AD.
ΔABC và ΔABD có:
AC = AD (=2cm)
BC = BD (=3cm)
AB cạnh chung
Nên ΔABC = ΔABD (c.c.c)
Suy ra góc CAB = góc DAB (góc tương ứng)
⇒ AB là tia phân giác của góc CAD
15 tháng 3 2016
∆BAC và ∆ BAD có: AC=AD(gt)
BC=BD(gt)
AB cạnh chung.
Nên ∆ BAC= ∆ BAD(c.c.c)
Suy ra BAC = BAD (góc tương ứng)
Vậy AB là tia phân giác của góc CAD
CT
15 tháng 11 2018
Noi AC ;BC;AD;BD
Xét tam giác ACB và tam giác ADB , ta co:\
CA=AD ( BK của A )
CB=DB (BK cua B )
Canh AB chung
=>tam giac ACB=tam giac ADB (c.c.c)
=>goc CAB =goc BAD
ma tia AB nam giua 2 tia AC,AD
=>tia AB la phan giac cua goc CAD
18 tháng 10 2017
Xét có :
AB chung
AC = AD (gt)
BC=BD
=> tam giác BAC = BAD ( c.c.c )
=> góc BAC = BAD ( 2 góc tương ứng)
=> AB là tia phân giác của góc CAD
15 tháng 11 2017
Vì C là giao của đường tròn tâm A và tâm B nên AC=2cm,BC=3cm
Vì D là giao của đường tròn tâm A và tâm B nên AD=2cm,BD=3cm
Do đó AC=AD,BC=BD
Xét ΔBAC và ΔBAD có:
+) AC=AD
+) BC=BD
+) AB cạnh chung.
Suy ra ΔBAC=ΔBAD(c.c.c)
Suy ra ˆBAC = ˆBAD (hai góc tương ứng)
Vậy AB là tia phân giác của góc CAD
cảm ơn bn nha