Cho Δ ABC, có góc A = 70o, góc C = 30o. Tia phân giác của góc B cắt AC ở D.
a) Tính góc ABC và góc ADB;
b) Tia phân giác của góc C cắt AB ở E và cắt BD ở I . Tính góc BIC và góc CID.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 10 2021
a: \(\widehat{ABC}=80^0\)
\(\widehat{ADB}=180^0-70^0-40^0=70^0\)
KV
18 tháng 12 2022
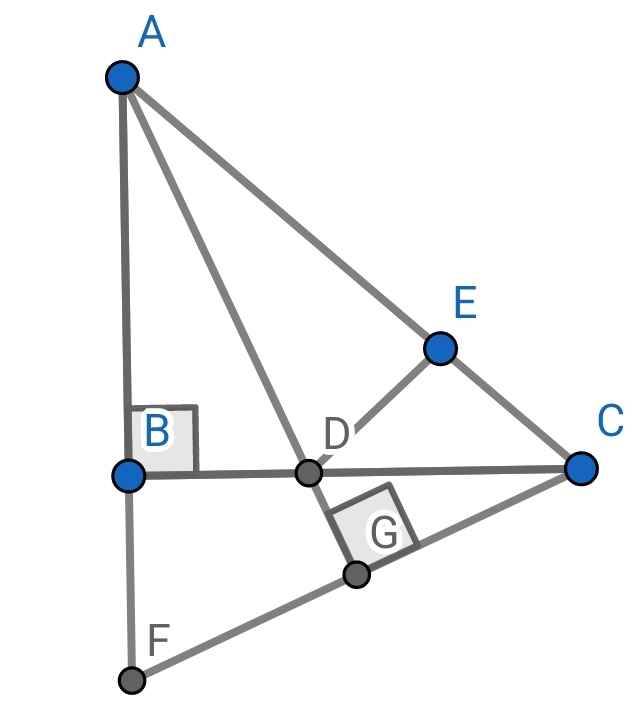
a) Xét ∆ADB và ∆ADE có:
AD chung
Góc BAD = góc EAD (AD là tia phân giác của góc BAC)
AB = AE (gt)
⇒∆ADB = ∆ADE (c-g-c)
b) Do ∆ADB = ∆ADE (c-g-c)
⇒góc ABD = góc AED (hai góc tương ứng)
⇒góc AED = 90⁰
Hay DE vuông góc AC
c) Gọi G là giao điểm của CF và AD
Do góc BAD = góc EAD (cmt)
⇒góc FAG = góc CAG
Xét hai tam giác vuông: ∆AGF và ∆AGC có:
AG chung
góc FAG = góc CAG (cmt)
⇒∆AGF = ∆AGC (cạnh góc vuông - góc nhọn kề)
⇒AF = AC (hai cạnh tương ứng)
Mà AF = AB + BF
AC = AE + EC
AB = AE
⇒BF = CE
CM
7 tháng 7 2017
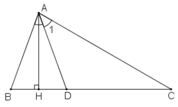
Ta có: ∠(A1 ) =(1/2 )∠(BAC) = (1/2).80o = 40o
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có ∠(ADH) là góc ngoài tại đỉnh D
Do đó: ∠(ADH) = ∠(A1) + ∠C (tính chất góc ngoài của tam giác)
Vậy ∠(ADH ) = 40o + 30o = 70o
CM
9 tháng 8 2019
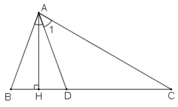
ΔADH vuông tại H nên:
∠(HAD) + ∠(ADH) = 90o (tính chất tam giác vuông)
⇒∠ (HAD) = 90o-∠(ADH)o = 90o - 70o = 20o
CM
3 tháng 2 2019
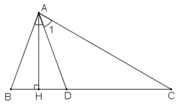
Trong ΔABC có:
∠(BAC) + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Mà ∠(BAC) + 70o + 30o = 180
Vậy ∠(BAC) = 180o-70o - 30o = 80o
a)góc abc=180-70-30=80
góc adb=180-70-(80:2)=70
pgiac nê góc chia hai
b)góc bic=180-(80:2)-(30:2)=125
pgiac nên góc chia hai
góc cid=180-125=55(kề bù)