câu 1: cho tứ giác ABCD. Gọi O là trung điểm của AB.Chứng minh rằng: \(\overrightarrow{OD}+\overrightarrow{OC}=\overrightarrow{AD}+\overrightarrow{BC}\)Câu 2: Cho tam giác ABC. Gọi A' là điểm đối xứng của B qua A, B' là điểm dối xứng của C qua B, C' là điểm đối xứng của A qua C. Với một điểm O bất kì, chứng minh...
Đọc tiếp
câu 1: cho tứ giác ABCD. Gọi O là trung điểm của AB.
Chứng minh rằng: \(\overrightarrow{OD}+\overrightarrow{OC}=\overrightarrow{AD}+\overrightarrow{BC}\)
Câu 2: Cho tam giác ABC. Gọi A' là điểm đối xứng của B qua A, B' là điểm dối xứng của C qua B, C' là điểm đối xứng của A qua C. Với một điểm O bất kì, chứng minh rằng:
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OA'}+\overrightarrow{OB'}+\overrightarrow{OC'}\)
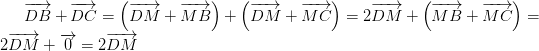
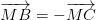
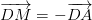
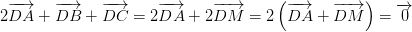
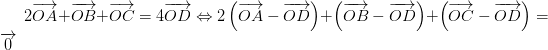
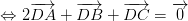luôn đúng theo câu a
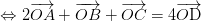, với O là điểm tùy ý
câu 2 ( các kí hiệu vecto khi lm bài thỳ b tự viết nhé mk k viết kí hiệu để trả lời cho nhanh hỳ hỳ )
OA+ OB + OC = OA'+ OB' + OC'
<=> OA - OA' + OB - OB' + OC - OC' = 0
<=> A'A + B'B + C'C = 0
<=> 2 ( BA + CB + AC ) = 0
<=> 2 ( CB + BA + AC ) = 0
<=> 2 ( CA + AC ) = 0
<=> 0 = 0 ( luôn đúng )
câu 1 ( các kí hiệu vecto b cx tự viết nhá )
VT = OD + OC = OA + AD + OB + BC = OA + OB + AD + BC = BO + OB + AD + BC = 0 + AD + BC = AD + BC = VP ( đpcm)