cho tam giác ABC vuông tại A đường phân giác BD vẽ DH cắtBC
chứng minh
a tam giác ABD = tam giác HBD
b bd là đường trung trực của AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 7 2023
a: Xét ΔABD vuông tạiA và ΔHBD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: BA=BH
DA=DH
=>BD là trung trực của AH
c: Xét ΔDAK và ΔDHC có
DA=DH
góc ADK=góc HDC
DK=DC
=>ΔDAK=ΔDHC
=>góc DAK=góc DHC=90 độ
=>góc DAK+góc DAB=180 độ
=>B,A,K thẳng hàng
16 tháng 4 2022
a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
b: Ta có: ΔBAH cân tại B
mà BM là phân giác
nên BM là đường trung tuyến
Xét ΔBAH có
BM là đường trung tuyến
AK là đường trung tuyến
BM cắt AK tại I
Do đó; I là trọng tâm của ΔBAH
KV
2 tháng 5 2023
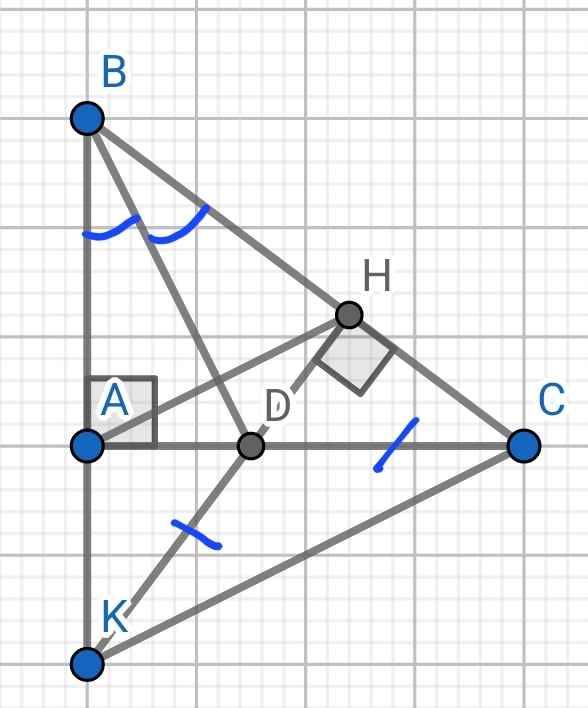
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng
HA
13 tháng 6 2020
A)XÉT \(\Delta ABD\)VÀ\(\Delta HBD\)CÓ
\(\widehat{BAD}=\widehat{BHD}=90^o\)
\(\widehat{ABD}=\widehat{DBH}\left(GT\right)\)
BD LÀ CẠNH CHUNG
=>\(\Delta ABD\)=\(\Delta HBD\)(CẠNH HUYỀN - GÓC NHỌN ) ( ĐPCM)
GỌI I LÀ GIAO ĐIỂM CỦA BD VÀ AH
XÉT \(\Delta ABI\)VÀ\(\Delta HBI\)CÓ
\(AB=BH\left(\Delta ABD=\Delta HBD\right)\)
\(\widehat{ABD}=\widehat{DBH}\left(GT\right)\)
BI LÀ CẠNH CHUNG
=>\(\Delta ABI\)=\(\Delta HBI\)(C-G-C)
\(\Rightarrow\widehat{AIB}=\widehat{HIB}\)( HAI GÓC TƯƠNG ỨNG)
MÀ HAI GÓC NÀY KỀ BÙ
\(\Rightarrow\widehat{AIB}=\widehat{HIB}=\frac{180^o}{2}=90^o\left(1\right)\)
mà\(\Delta ABI\)=\(\Delta HBI\)(C-G-C)
=> AI=HI( HAI CẠNH TƯƠNG ỨNG ) (2)
TỪ 1 VÀ 2 => BI LÀ ĐƯỜNG TRUNG TRỰC CỦA AH HAY BD LÀ ĐƯỜNG TRUNG TRỰC CỦA AH(ĐPCM)
B)
b)
Vì \(\Delta\)DBA =\(\Delta\) DBH ( cm ở câu a )
=) AD = DH
Xét\(\Delta\)DHC ( DHC = 90 ) có :
DC là cạnh huyền
\(\Rightarrow\) DC là cạnh lớn nhất
\(\Rightarrow DC>DH\)
mà DH = AD
\(\Rightarrow AD< DC\)
NH
13 tháng 6 2020
a, Xét △ABD vuông tại A và △HBD vuông tại H
Có: BD là cạnh chung
ABD = HBD (gt)
=> △ABD = △HBD (ch-gn)
=> AB = BH (2 cạnh tương ứng) => B thuộc đường trung trực của AH
và AD = HD (2 cạnh tương ứng) => D thuộc đường trung trực của AH
=> BD là đường trung trực của AH
b, Xét △HDC vuông tại H có: DC > DH (quan hệ giữa đường xiên và đường vuông góc)
=> DC > AD
17 tháng 2 2022
a: Xét ΔBAD và ΔBHD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔBAD=ΔBHD
Suy ra: \(\widehat{BAD}=\widehat{BHD}=90^0\)
hay DH\(\perp\)BC
b: Xét ΔADK vuông tại A và ΔHDC vuông tại H có
DA=DH
\(\widehat{ADK}=\widehat{HDC}\)
Do đó: ΔADK=ΔHDC
Suy ra: AK=HC
Ta có: BA+AK=BK
BH+HC=BC
mà BA=BH
và AK=HC
nên BK=BC
=>ΔBKC cân tại B
mà BD là phân giác
nên BD là đường trung trực của KC
9 tháng 3 2022
a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
