Một chuyển động trong nửa đầu quãng đường , chuyển động có vận tốc không đổi V1 , trong nửa quãng đường còn lại có vận tốc V2 . Tính vận tốc trung bình của nó trên cả quãng đường . Chứng tỏ vận tốc trung bình này không lớn hơn trung bình cộng cảu hai vận tốc V1 và V2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
13 tháng 10 2021
ta có:
t1=S1v1=S2v1S1v1=S2v1
t2=S2v2=S2v2t2=S2v2=S2v2
vận tốc trung bình của nhười đó là:
vtb=St1+t2=SS2v1+S2v2=112v1+12v2=1v2+v12v1v2=2v1v2v2+v1vtb=St1+t2=SS2v1+S2v2=112v1+12v2=1v2+v12v1v2=2v1v2v2+v1
lấy vtb-trung bình cộng 2 v ta có:
2v1v2v1+v2−v1+v22=4v1v2−v21−2v1v2−v222(v1+v2)=−(v21−2v1v2+v22)2(v1+v2)2v1v2v1+v2−v1+v22=4v1v2−v12−2v1v2−v222(v1+v2)=−(v12−2v1v2+v22)2(v1+v2)
=−(v1−v2)22(v1+v2)=−(v1−v2)22(v1+v2)
mà (v1-v2)2>0 nên
-(v1-v2)2<0 và 2*(v2+v1)>0 nên ta suy ra
vận tốc trung bình này ko bao giờ lớn hơn trung bình cộng của hai vận tốc v1 và v2
B
17 tháng 8 2020
Bài làm :
Gọi thời gian đi hết cả đoạn đường là 2t
Ta có :
S = v1t + v2t = t(v1 + v2 )
Vậy vận tốc trung bình trên cả quãng đường là :
\(V_{TB}=\frac{S}{2t}=\frac{t\left(v_1+v_2\right)}{2t}=\frac{v_1+v_2}{2}\)
Chúc bạn học tốt !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
TM
17 tháng 8 2020
Ta có :
\(t1=\frac{S1}{v1}=\frac{S}{2v1}\)
\(t2=\frac{S2}{v2}=\frac{S}{2v2}\)
Vận tốc trung bình của người đó là :
\(Vtb=\frac{S}{t1+t2}\times\frac{S}{\frac{S}{2v1}+\frac{S}{2v2}}=\frac{1}{\frac{1}{2v1}+\frac{1}{2v2}}=\frac{1}{\frac{v2+v1}{2v1v2}}\)
H9
HT.Phong (9A5)
CTVHS
18 tháng 6 2023
Gọi s là độ dài nửa quãng đường. Ta có thời gian đi nửa quãng đường đầu là:
\(t_1=\dfrac{s}{v_1}\)
Gọi thời gian ô tô đi nửa phần còn lại là \(t_2\) và \(t_3\) và \(t_2=t_3\)
Thời gian ô tô đi được trong mỗi đoạn này là:
\(s_2=v_2t_2\)
\(s_3=v_3t_3\)
Mà: \(t_2=t_3=\dfrac{s}{v_2+v_3}\)
Vận tốc \(v_3\) là:
\(v_{tb}=\dfrac{2v_1\left(v_2+v_3\right)}{v_2+v_3+2v_1}\) hay \(40=\dfrac{2\cdot30\cdot\left(45+v_3\right)}{45+v_3+2\cdot30}\)
\(\Leftrightarrow40=\dfrac{60\left(45+v_3\right)}{105+v_3}\)
\(\Leftrightarrow40\left(105+v_3\right)=60\left(45+v_3\right)\)
\(\Leftrightarrow2\left(105+v_3\right)=3\left(45+v_3\right)\)
\(\Leftrightarrow210+2v_3=135+3v_3\)
\(\Leftrightarrow3v_3-2v_3=210-135\)
\(\Leftrightarrow v_3=75\left(km/h\right)\)
24 tháng 12 2021
a) Thời gian vật đi hết quãng đường trên:
\(t_{tổng}=t_1+t_2=\dfrac{S_1}{v_1}+\dfrac{S_2}{v_2}=\dfrac{520:2}{5}+\dfrac{520:2}{7}=\dfrac{624}{7}\left(s\right)\)
b) Thời gian vật đi quãng đường T1 và quãng đường T2:
\(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{520:2}{5}=52\left(s\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{520:2}{7}=\dfrac{260}{7}\left(\dfrac{m}{s}\right)\end{matrix}\right.\)
Vận tốc trung bình trên cả quãng đường:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{520}{52+\dfrac{260}{7}}=\dfrac{35}{6}\left(\dfrac{m}{s}\right)\)
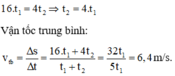
ta có:
t1=\(\frac{S_1}{v_1}=\frac{S}{2v_1}\)
\(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\)
vận tốc trung bình của nhười đó là:
\(v_{tb}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{2v_1}+\frac{S}{2v_2}}=\frac{1}{\frac{1}{2v_1}+\frac{1}{2v_2}}=\frac{1}{\frac{v_2+v_1}{2v_1v_2}}=\frac{2v_1v_2}{v_2+v_1}\)
lấy vtb-trung bình cộng 2 v ta có:
\(\frac{2v_1v_2}{v_1+v_2}-\frac{v_1+v_2}{2}=\frac{4v_1v_2-v_1^2-2v_1v_2-v_2^2}{2\left(v_1+v_2\right)}=\frac{-\left(v_1^2-2v_1v_2+v_2^2\right)}{2\left(v_1+v_2\right)}\)
\(=\frac{-\left(v_1-v_2\right)^2}{2\left(v_1+v_2\right)}\)
mà (v1-v2)2>0 nên
-(v1-v2)2<0 và 2*(v2+v1)>0 nên ta suy ra
vận tốc trung bình này ko bao giờ lớn hơn trung bình cộng của hai vận tốc v1 và v2
cái chỗ vận tốc tb-tbc 2 v là 4v1v2- v1mũ 2 đúng ko