Question

[Nguyễn Thị Quỳnh Như]

Cho hàm số \(y=\frac{mx+1}{x+m-2}\), có đồ thị là  \(\left(C_m\right)\) 

a. Viết phương trình tiếp tuyến của  \(\left(C_1\right)\) , biết tiếp tuyến đi qua điểm P(3;1)

b. Viết phương trình tiếp tuyến của  \(\left(C_1\right)\) , biết tiếp tuyến đi qua điểm A(2;-1)

c. Tìm m để tiếp tuyến tại điểm có hoành độ x = 1 vuông góc với đường thẳng y = x +1

Answer 1

[Trần Minh Ngọc]

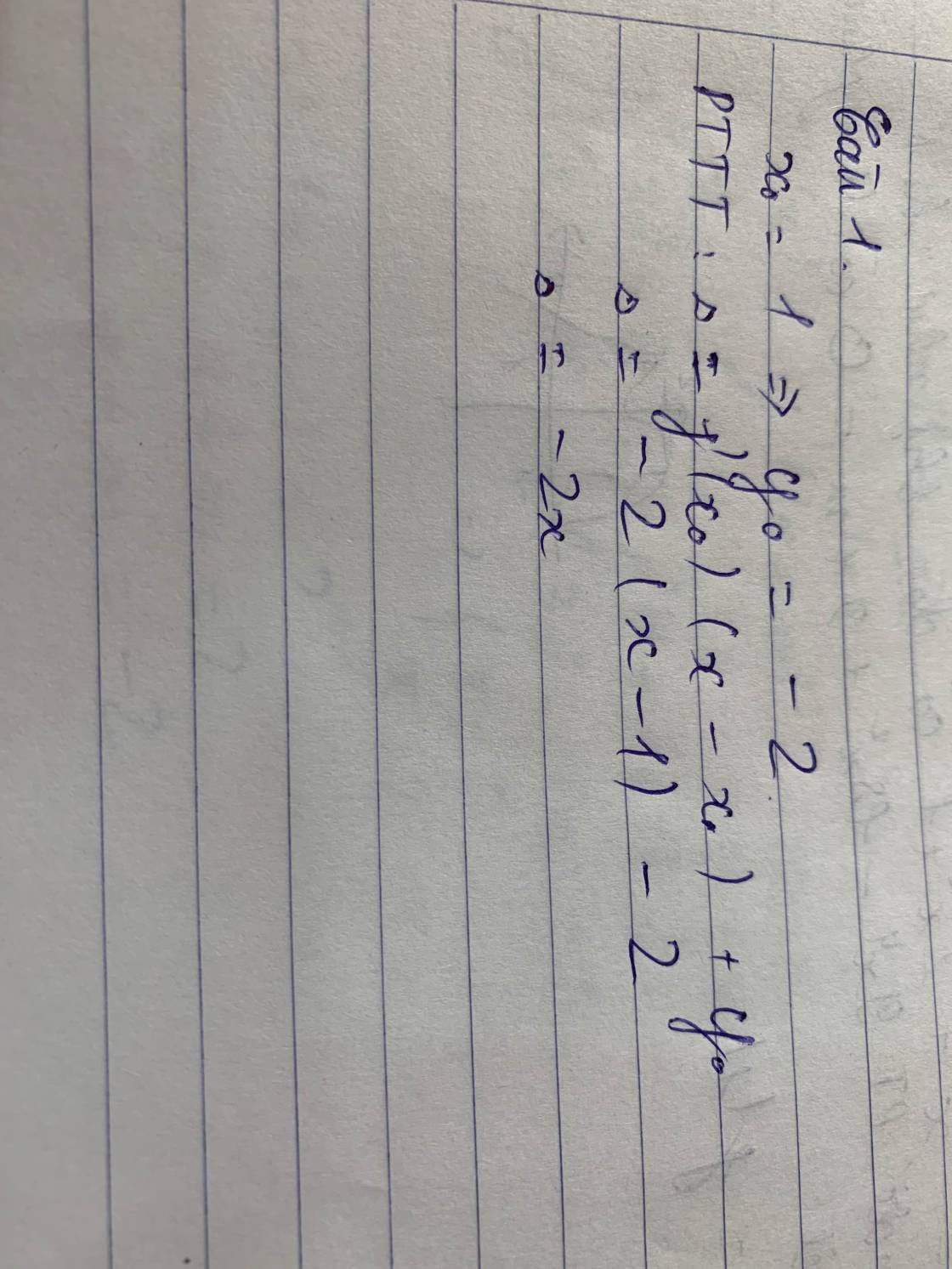
Với m = 1, ta có \(\left(C_1\right):y=\frac{x+1}{x-1}\)

a. Gọi d là đường thẳng đi qua P, có hệ số góc k => \(d:y=k\left(x-3\right)+1\)

d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-3\right)+1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm

Thế k vào phương trình thứ nhất, ta được :

\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-3\right)+1\Leftrightarrow x=2\)

\(\Rightarrow k=-2\Rightarrow\) phương trình tiếp tuyến : \(y=-2x+7\)

b. Gọi d là đường thẳng đi qua A, có hệ số góc k : \(d:y=k\left(x-2\right)-1\)

d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=k\left(x-2\right)-1\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm

Thế k vào phương trình thứ nhất, ta được :

\(\frac{x+1}{x-1}=\frac{-2}{\left(x-1\right)^2}\left(x-2\right)-1\Leftrightarrow x=\pm\sqrt{2}\)

* \(x=\sqrt{2}\Rightarrow k=-2\left(3+2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3+2\sqrt{2}\right)x+11+8\sqrt{2}\)

* \(x=-\sqrt{2}\Rightarrow k=-2\left(3-2\sqrt{2}\right)\Rightarrow\) phương trình tiếp tuyến : \(y=-2\left(3-2\sqrt{2}\right)x+11-8\sqrt{2}\)

 c. Ta có : \(y'=\frac{m^2-2m-1}{\left(x+m-2\right)^2}\)Tiếp tuyến tại điểm có hoành độ x = 1 vuông góc với đường thẳng\(y=x+1\Leftrightarrow y'\left(1\right)=-1\Leftrightarrow\frac{m^2-2m-1}{\left(m-1\right)^2}=-1\)\(\Leftrightarrow m=0;m=2\)