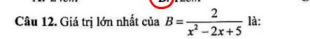Giải giúp em c,d vớ ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Trần Thành Đạt
28 tháng 7 2021
Đúng(1)
Những câu hỏi liên quan
RH
15 tháng 12 2021
B lớn nhất khi x^2 - 2x + 5 nhỏ nhất.
Ta có: x^2 - 2x + 5 = (x - 1)^2 + 4 >= 4
--> x^2 - 2x + 5 nhỏ nhất bằng 4 (khi x = 1)
--> B lớn nhất bằng 2/4 = 1/2 (khi x = 1)
L
15 tháng 12 2021
\(B=\dfrac{2}{x^2-2x+5}\)
Ta có:
\(x^2-2x+5\\ =\left(x^2-2x+4\right)-4+5\\ =\left(x-2\right)^2+1\)
Vì \(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-2\right)^2+1\ge1\forall x\\ \Rightarrow\dfrac{2}{\left(x-2\right)^2+1}\le2\forall x\\ \Rightarrow B\le2\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\\ \Leftrightarrow x=2\)
Vậy GTLN của B là 2 <=> x =2
DT
Đỗ Thanh Hải
CTVVIP
27 tháng 5 2021
1 inheritance
2 dental
3 fascinating
4 confidence
5 amazement
6 Surprisingly
7 depressed
8 dissatisfication
9 laziness
10 admiration
HK
1
NH
20 tháng 12 2019
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{d}{a}=\frac{a+b+c+d}{b+c+d+a}=1\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{b}=1\\\frac{b}{c}=1\\\frac{c}{d}=1\end{cases}}\Rightarrow\hept{\begin{cases}a=b\\b=c\\c=d\end{cases}}\Rightarrow a=b=c=d\)
Ta có: \(VT=a.b^{19}.c^{1999}=d.d^{19}.d^{1999}=d^{2019}=VP\)(đpcm)
VD
11 tháng 1 2021
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
0H
Chỉ cần giải giúp em câu c,d thui ạ
1
24 tháng 5 2022
a: Xét ΔEAB có \(\widehat{EBA}=\widehat{EAB}\)
nên ΔEAB cân tại E
mà EK là đường cao
nen K là trung điểm của AB
hay KA=KB
b: Xét ΔACE vuông tại C và ΔBDE vuông tại D có
EA=EB
\(\widehat{AEC}=\widehat{BED}\)
Do đó: ΔACE=ΔBDE
Suy ra: EC=ED
Ta có: AE+ED=AD
BE+CE=BC
mà AE=BE
và ED=EC
nên AD=BC
