Một vật dao động điều hoà trong 1 phút thực hiện được 50 dao động và đi được quãng đường là 16m. Tính tốc độ trung bình bé nhất mà vật có thể đạt được trong khoảng thời gian dao động bằng 1,6 s?
A.15 cm/s.
B.18 cm/s.
C.20 cm/s.
D.25 cm/s.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
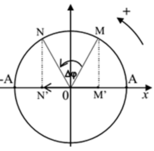
Ta dựa vào tính chất của dao động là vật chuyển động càng nhanh khi càng gần vị trí cân bằng cho nên quãng đường dài nhất DS vật đi được trong thời gian Dt với 0 < Dt < T/2 phải đối xứng qua vị trí cân bằng (hình vẽ)
![]()
Với thời gian t = 2T/3 = T/2 + T/6 → S = 2A + ∆S (∆φ = 60o)
Do vậy, tốc độ trung bình lớn nhất của vật thực hiện được trong khoảng thời gian 2T/3 khi vật đi được quảng đường lớn nhất trong khoảng thời gian 2T/3 →∆S phải lớn nhất
→ ![]() = 2A.sin(60/2) = A →Smax = 3A
= 2A.sin(60/2) = A →Smax = 3A
→ tốc độ trung bình lớn nhất = Smax / t = 9A/2

Đáp án A
Dựa vào mối quan hệ giữa chuyển động tròn đều và dao động điều hòa ta thấy: trong khoảng thời gian T 4 ứng với góc quay π 2 . Giả sử ban đầu vật ở M ứng với góc a, sau t = T 4 vật ở N ứng với góc b ( β = π 2 - α ), quãng đường đi tương ứng của vật là:
![]()
![]()
![]()
![]()
![]()
Từ đó: ![]()
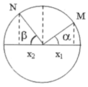
Tốc độ trung bình \(v = \frac{\text{quãng đường đi được}}{t} \)
Vời thời gian t = 1,6s là không đối tức là \(v_{min} <=> S_{min}\)
Ta có: \(T = \frac{60s}{50} = 1,2s ; A = \frac{16}{2} = 8cm.\)
Nhận xét \(t = 1,6 > T/2 = 0.6 \) nên ta tách: \(t = 2.0,6+0.4 = 2.t_1+t_2\)
Ta sẽ đi tìm quãng đường nhỏ nhất ứng với thời gian \(t_1 = 0.6 s\). Để tìm được quãng đường nhỏ nhất ứng với \(t_1 = 0.6 s\) ta sẽ dùng đường tròn và quỹ đạo của vật sẽ lấy vị trí biên làm trung điểm. Tức là
Góc quay đương ưng với \(t_1 = 0.6 s\) là \(\varphi _1 = t_1 \omega = 0.6\frac{2\pi}{1,2} = \pi.\) Cung quay được sẽ lấy biên làm trung điểm tức là cung \(\stackrel\frown{MaN} = \pi\)
=> \(S_{1min} = 2. A. (1)\) (2 lần đoạn màu đỏ trên hình ứng với đi từ N đến biên A rồi từ biên A đến điểm M)
Chú ý là quãng đường đường đi được trong t = T/2 thì luôn luôn là 2A. Nên có thể không cần tính mà áp dụng luôn.
Tương tự ta sẽ tìm quãng đường nhỏ nhất ứng với thời gian \(t_2 = 0.4 s\) => \(\varphi _2 = t_2 \omega = 0.4\frac{2\pi}{1,2} = \frac{2\pi}{3}.\)
=> \(S_{2min} = 2. (A - \frac{A}{2} ). (2)\) (2 lần đoạn màu đỏ trên hình ứng với đi từ Q đến biên A rồi từ biên A đến điểm P)
Từ (1) và (2) ta thu được \(v_{min} = \frac{S_{min}}{t} = \frac{2S_{1}+S_2}{t} = \frac{4A+2(A-\frac{A}{2})}{1,6} = \frac{A. (6-1)}{1,6} =25 cm/s.\)
Như vậy đáp án thu được là D. 25cm/s.