Trong thí nghiệm giao thoa ánh sáng, nguồn S phát bức xạ lam đa; D không đổi; a có thể thay đổi nhưng S1,S2 luôn cách đều S. Xét M trên màn lúc đầu là vân sáng 4 nếu lần lượt giảm hoặc tăng S1;S2 1 lượng đenta a thì tại đó vân sáng bậc k và 3k. Nếu tăng S1;S2 thêm 2đenta a thì tại M sẽ là:
A.vân tối 9
B.vân sáng 9
C.vân sáng 7
D.vân sáng 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Khoảng vân: 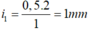
⇒ Số vân sáng của bức xạ λ1 là:
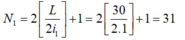
- Khoảng vân: 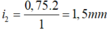
⇒ Số vân sáng của bức xạ λ2 là:
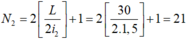
- Vị trí vân sáng của hai bức xạ λ1 và λ2 trùng nhau thoả mãn:
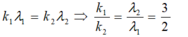
⇒ Khoảng vân trùng:
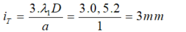
⇒ Số vân sáng trùng nhau của hai bức xạ là:
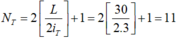
- Vậy số vạch màu quan sát được trên vùng giao thoa:
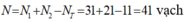

Đáp án A
Phương pháp: Công thức tính số vân sáng trên bề rộng miền giao thoa L:

Vị trí vân sáng của hai bức xạ λ 1 và λ 2 trùng nhau thoả mãn:

=> Số vân sáng trùng nhau của hai bức xạ là:
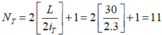
Vậy số vạch màu quan sát được trên vùng giao thoa:
![]()

Đáp án A
Phương pháp: Công thức tính số vân sáng trên bề rộng miền giao thoa L:
Cách giải:
+ Khoảng vân 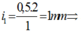 Số vân sáng của bức xạ λ1 là:
Số vân sáng của bức xạ λ1 là:
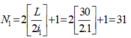
Khoảng vân ![]() Số vân sáng của bức xạ λ2 là:
Số vân sáng của bức xạ λ2 là:
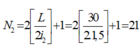
Vị trí vân sáng của hai bức xạ λ1 và λ2 trùng nhau thoả mãn:
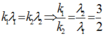
=> Khoảng vân trùng:
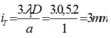
=> Số vân sáng trùng nhau của hai bức xạ là:
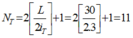
Vậy số vạch màu quan sát được trên vùng giao thoa: N = N1 + N2 – NT = 31+21 – 11 = 41 vạch

Đáp án D
Phương pháp: Vị trí vân trùng nhau:
![]()
Cách giải:
Vị trí trùng nhau của ánh sáng đỏ và lam:
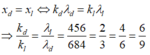
Trong khoảng giữa hai vân sáng có màu cùng màu với vân sáng trung tâm có 6 vân màu lam => kl chạy từ 0 đến 9
Ta có bảng sau:
k l |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
k d |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|||
=> Có 3 vân sáng màu đỏ (ứng với k = 1; 3; 5)

Đáp án D
Phương pháp: Vị trí vân trùng nhau: x1 = x2 <=> k1λ1 = k2λ2
Cách giải:
Vị trí trùng nhau của ánh sáng đỏ và lam:
![]()
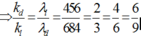
Trong khoảng giữa hai vân sáng có màu cùng màu với vân sáng trung tâm có 6 vân màu lam => kl chạy từ 0 đến 9
Ta có bảng sau:
| kl |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| kd |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|||
=> Có 3 vân sáng màu đỏ (ứng với k = 1; 3; 5)

Đáp án A
+ Lần thứ nhất: Ánh sáng dùng trong thí nghiệm có hai loại bức xạ λ 1 = 0,5µm và λ 2
- Trong khoảng giữa hai vân sáng cùng màu với vạch sáng trung tâm có 4 vạch màu của λ 2 => vị trí vân trùng của 2 bức xạ ứng với vị trí vân sáng bậc 5 của λ 2 :
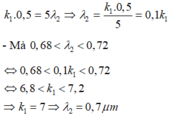
+ Lần thứ 2: Ánh sáng dùng trong thí nghiệm có ba loại bức xạ λ 1 = 0,5µm và λ 2 = 0,7µm và
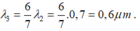
- Vị trí vân sáng trùng nhau của 3 bức xạ thoả mãn:
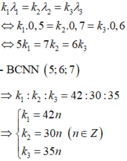
- Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có tổng 41 vân sáng của λ 1 ; 29 vân sáng của λ 1 ; 34 vân sáng của λ 3
=> Tổng số vân sáng của 3 bức xạ là: N = 41 + 29 + 34 = 104 vân. (*)
- Số vân sáng trùng nhau của hai bức xạ λ 1 và λ 2 :
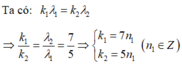
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 5 vân trùng nhau của hai bức xạ λ 1 và λ 2 (ứng với n 1 = 1; 2; 3; 4; 5). (**)
- Số vân sáng trùng nhau của hai bức xạ λ 1 và λ 3 :
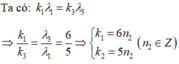
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 6 vân trùng nhau của hai bức xạ λ 1 và λ 3 (ứng với n 2 = 1; 2; 3; 4; 5; 6). (***)
- Số vân sáng trùng nhau của hai bức xạ λ 2 và λ 3 :
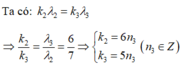
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 4 vân trùng nhau của hai bức xạ λ 2 và λ 3 (ứng với n 3 = 1; 2; 3; 4). (****)
Từ (*),(**),(***),(****) => số vạch sáng đơn sắc quan sát được: Ns = N – 2(5 + 6 + 4) = 104 – 30 = 74.

Đáp án A
+ Lần thứ nhất: Ánh sáng dùng trong thí nghiệm có hai loại bức xạ λ1 = 0,5µm và λ2
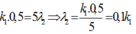
- Trong khoảng giữa hai vân sáng cùng màu với vạch sáng trung tâm có 4 vạch màu của λ2 => vị trí vân trùng của 2 bức xạ ứng với vị trí vân sáng bậc 5 của λ2 :
- Mà ![]()
![]()
+ Lần thứ 2: Ánh sáng dùng trong thí nghiệm có ba loại bức xạ λ1 = 0,5µm
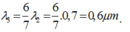
- Vị trí vân sáng trùng nhau của 3 bức xạ thoả mãn:
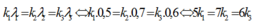
- BCNN(5;6;7) 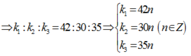
- Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có tổng 41 vân sáng của λ1; 29 vân sáng của λ1; 34 vân sáng của λ3
=> Tổng số vân sáng của 3 bức xạ là: N = 41 + 29 + 34 = 104 vân. (*)
- Số vân sáng trùng nhau của hai bức xạ λ1 và λ2:
Ta có: 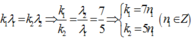
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 5 vân trùng nhau của hai bức xạ λ1 và λ2 (ứng với n1 = 1; 2; 3; 4; 5). (**)
- Số vân sáng trùng nhau của hai bức xạ λ1 và λ3:
Ta có: 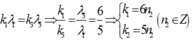
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 6 vân trùng nhau của hai bức xạ λ1 và λ3 (ứng với n2 = 1; 2; 3; 4; 5; 6). (***)
- Số vân sáng trùng nhau của hai bức xạ λ2 và λ3:
Ta có: 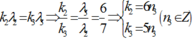
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 4 vân trùng nhau của hai bức xạ λ2 và λ3 (ứng với n3 = 1; 2; 3; 4). (****)
Từ (*),(**),(***),(****) => số vạch sáng đơn sắc quan sát được: Ns = N – 2(5 + 6 + 4) = 104 – 30 = 74.


Ta có: \(x_M=k.i=k.\frac{\lambda D}{a}\Rightarrow x_M.a=k.\lambda D\)
Theo giả thiết ta có:
\(x_M.a=4.\lambda D\)(1)
\(x_M.\left(a-\Delta a\right)=k.\lambda D\)(2)
\(x_M.\left(a+\Delta a\right)=3k.\lambda D\)(3)
Lần lượt chia vế với vế của (3) với (2) ta đc:
\(\frac{a+\Delta a}{a-\Delta a}=3\Rightarrow\Delta a=\frac{a}{2}\)
Nếu tăng S1S2 thêm 2\(\Delta a\) thì S1S2 = a' = a + 2.a/2=2a.
Khi đó: \(x_M\left(2a\right)=8.\lambda D\Rightarrow x_M=8.\frac{\lambda D}{a'}\)
Như vậy tại M là vân sáng bậc 8.
Chọn đáp án D.