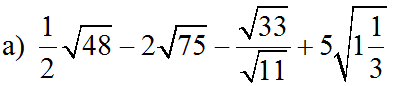
giải chi tiết từng bước giúp mình với mình đang cần gấp lắm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
2
19 tháng 7 2021
b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
LN
19 tháng 7 2021
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)
DD
Đoàn Đức Hà
Giáo viên
28 tháng 3 2021
\(A=\frac{1\times111+2\times110+3\times109+...+111\times1}{1+\left(1+2\right)+\left(1+2+3\right)+...+\left(1+2+3+...+111\right)}\)
\(A=\frac{1\times111+2\times110+3\times109+...+111\times1}{\left(1+1+...+1\right)+\left(2+2+...+2\right)+...+111}\)(\(111\)số hạng \(1\), \(110\)số hạng \(2\),...)
\(A=\frac{1\times111+2\times110+3\times109+...+111\times1}{1\times111+2\times110+3\times109+...+111\times1}\)
\(A=1\)
3 tháng 8 2018
a) \(\left(a+b-c\right)^2-\left(a-c\right)^2-2ab+2ac\)
\(=a^2+b^2+c^2+2ab-2bc-2ac-a^2+2ac-c^2-2ab+2ac\)
\(=b^2-2bc+2ac=b.\left(b-2c+2a\right)\)
b) \(x^4+2x^3+5x^2+4x-12\)
\(=x^4-x^3+3x^3-3x^2+8x^2-8x+12x-12\)
\(=x^3.\left(x-1\right)+3x^2.\left(x-1\right)+8x.\left(x-1\right)+12.\left(x-1\right)\)
\(=\left(x-1\right)\left(x^3+3x^2+8x+12\right)\)
\(=\left(x-1\right)\left[\left(x^3+2x^2\right)+\left(x^2+2x\right)+\left(6x+12\right)\right]\)
\(=\left(x-1\right)\left[x^2.\left(x+2\right)+x.\left(x+2\right)+6.\left(x+2\right)\right]\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+6\right)\)
NB
3 tháng 8 2018
Pạn Khánh Châu ơi
Cái dòng thứ 2 đấy, dấu hiệu nhận biết là j vậy
Mà sao pạn phân tích hay vậy????
HA
0
18 tháng 9 2021
\(4,\\ 2.B=\sqrt{x}-1+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\left(x>0\right)\\ B=\dfrac{x-\sqrt{x}+2-2\sqrt{x}}{\sqrt{x}}=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\)
\(3.x=\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}=\left(3+\sqrt{2}\right)+\left(3-\sqrt{2}\right)=6\)
Thay vào B, ta được \(B=\dfrac{6-3\sqrt{6}+2}{\sqrt{6}}=\dfrac{6\sqrt{6}-18+2\sqrt{6}}{6}=\dfrac{4\sqrt{6}-9}{3}\)
\(4.B=0\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}=0\Leftrightarrow x-3\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
\(7.B\in Z\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}-3+\dfrac{2}{\sqrt{x}}\in Z\\ \Leftrightarrow\dfrac{2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow x\in\left\{1;4\right\}\left(\sqrt{x}>0\right)\)
T
1
O
22 tháng 3 2022
c) \(\left(\dfrac{1}{2}\cdot x+\dfrac{1}{4}\right)\cdot\left(2x-\dfrac{1}{3}\right)=0\)
\(\dfrac{1}{2}\cdot x+\dfrac{1}{4}=0\)
\(\dfrac{1}{2}\cdot x=0-\dfrac{1}{4}\)
\(\dfrac{1}{2}\cdot x=-\dfrac{1}{4}\)
\(x=-\dfrac{1}{4}\div\dfrac{1}{2}\)
\(x=-\dfrac{1}{2}\)
\(2x-\dfrac{1}{3}=0\)
\(2x=0+\dfrac{1}{3}\)
\(2x=\dfrac{1}{3}\)
\(x=\dfrac{1}{3}\div2\)
\(x=\dfrac{1}{6}\)
\(\Rightarrow\) \(x=\) {\(-\dfrac{1}{2};\dfrac{1}{6}\)}
13 tháng 11 2021
2: Thay x=1 và y=-4 vào (d), ta được:
2m+2=-4
hay m=-3
AH
Akai Haruma
Giáo viên
12 tháng 1 2022
Lời giải:
a. Mẹ An mua thực phẩm hết số tiền là:
$3\times 120000+4\times 50000+20\times 3500+220000=850000$ (đồng)
b. Mẹ An mua thực phẩm và khẩu trang hết:
$850000+2\times 35000=920000$ (đồng)
a) Ta có: \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}\)
\(=\dfrac{1}{2}\cdot4\sqrt{3}-2\cdot5\sqrt{3}-\sqrt{3}+5\cdot\dfrac{2}{\sqrt{3}}\)
\(=-9\sqrt{3}+\dfrac{10}{\sqrt{3}}\)
\(=\dfrac{-27+10}{\sqrt{3}}=\dfrac{-17\sqrt{3}}{3}\)