Một mặt phẳng nghiêng một góc α = 300 với mặt phẳng nằm ngang và dài AB = l = 1m. Một vật khối lượng m= 1kg trượt không vận tốc đầu từ đỉnh A tới C thì dừng lại. Tính
a) Phản lực của mặt phảng nghiêng đối với vật
b) Vận tốc của vật tại B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2021
Định luật II Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m\cdot\overrightarrow{a}\)
Ox: \(Psin\alpha-F_{ms}=m\cdot a\)
Oy: \(N-Pcos\alpha=0\Rightarrow N=Pcos\alpha=mgcos\alpha\)
\(F_{ms}=\mu_1\cdot N=\mu_1\cdot mgcos\alpha\)
Gia tốc mặt phẳng nghiêng:
\(a=\dfrac{Psin\alpha-F_{ms}}{m}=\dfrac{mgsin\alpha-\mu_1mgcos\alpha}{m}=g\left(sin\alpha-\mu_1cos\alpha\right)=10\left(sin30-0,1cos30\right)\approx4,13\)m/s2
VT
9 tháng 5 2017
Đáp án: A
Phương trình động lực học:
Chiếu (1) lên phương song song với mặt phẵng nghiêng (phương chuyển động), chiều dương hướng xuống (cùng chiều chuyển động), ta có:
Psina – Fms = ma1
Chiếu (1) lên phương vuông góc với mặt phẵng nghiêng (vuông góc với phương chuyển động), chiều dương hướng lên, ta có:
N - Pcosa = 0
→ N = Pcosa = mgcosa
→ Fms = m1N = m1mgcosa.
Gia tốc trên mặt phẵng nghiêng:
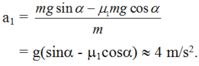
Vận tốc của vật tại B:
Gia tốc của vật trên mặt phẵng ngang:
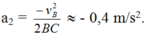
Trên mặt phẵng ngang ta có:
1 tháng 12 2018
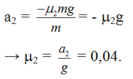
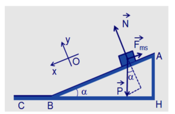
theo định luật II niu tơn trên mặt phẳng nghiêng AB
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương song song với mặt phẳng nằm nghiêng chiều dương cùng chiều chuyển động
\(sin\alpha.P-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương vuông gốc với mặt phẳng, chiều dương hướng lên trên
N=\(cos\alpha.P\) (3)
từ (2),(3)
\(\Rightarrow sin\alpha.g-\mu.g.cos\alpha=a\)
\(\Rightarrow a\approx4,1\)m/s2
vận tốc lúc vật tại B
\(v^2-v_0^2=2as_{AB}\Rightarrow v\approx2,875\)m/s
HQ
22 tháng 2 2021
a) Chọn mốc thế năng tại chân mặt phẳng nghiêng
Ta có: \(h=l.\sin\alpha=\dfrac{1}{2}.2=1\left(m\right)\)
Cơ năng tại A \(W_A=\dfrac{1}{2}mv_A^2+mgz_A=0+mgz_A=5\left(J\right)\)
Bỏ qua ma sát trên mặt phẳng nghiêng cơ năng của vật được bảo toàn: \(W_A=W_B=5\left(J\right)\)
b) Bảo toàn cơ năng: \(W_A=W_B\Leftrightarrow mgz_A=\dfrac{1}{2}mv_B^2\Leftrightarrow v_B=\sqrt{2gz_A}=2\sqrt{5}\left(m/s\right)\)
c) Ta có: \(-F_{ms}=ma\Rightarrow-\mu mg=ma\Rightarrow a=-1\left(m/s^2\right)\)
\(v_C^2-v_B^2=2aS\Rightarrow S=10\left(m\right)\)
VT
24 tháng 2 2017
Chọn mốc thế năng tại C (hình 95).
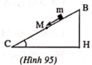
Cơ năng tại B: W B = m g h B
Cơ năng tại M: 
Công của lực ma sát: 
Định luật bảo toàn năng lượng:
VT
28 tháng 9 2017
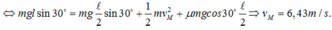
Ta có:
sin 30 = z s ⇒ z = s . sin 30 0 = 10. 1 2 = 5 ( m )
Chọn mốc thế năng tại chân dốc. Theo định luật bảo toàn cơ năng
W A = W B ⇒ m g z = 1 2 m v 2 ⇒ v = 2 g z ⇒ v = 2.10.5 = 10 ( m / s )
