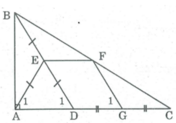
Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự
là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 4 2017
* Trong ∆ BDC, ta có:
E là trung điểm của BD (gt)
F là trung điểm của BC (gt)
Suy ra EF là đường trung bình của tam giác BCD
⇒ EF // DC hay EF // AG
Suy ra tứ giác AEFG là hình thang
G là trung điểm của DC (gt)
Nên FG là đường trung bình của tam giác BCD
⇒ FG // BD ⇒ ∠ G 1 = ∠ D 1 (đồng vị) (1)
* Trong tam giác ABD vuông tại A có AE là đường trung tuyến ứng với cạnh huyền BD
⇒ AE = ED = 1/2 BD (tính chất tam giác vuông)
Suy ra: tam giác AED cân tại E nên ∠ A 1 = ∠ D 1 (2)
Từ (1) và (2) suy ra: ∠ A 1 = ∠ G 1
Vậy hình thang AEFG là hình thang cân.
20 tháng 3 2020
Link ảnh: https://imgur.com/a/fYvijKU
Vì EF là đường trung bình của tam giác BDC nên EF//DC
Do đó: AEFG là hình thang
Do FG là đường trung bình của tam giác BDC nên FG//BD
=> \(\widehat{G_1}=\widehat{D_1}\)(đồng vị)
Tam giác ABD vuông tại A có AE là trung tuyến nên \(AE=\frac{BD}{2}=ED\)
Do đó tam giác AED cân tại E => \(\widehat{A_1}=\widehat{D_1}\)
Từ đó: \(\widehat{G_1}=\widehat{A_1}\)
Hình thang AEFG có 2 góc kề 1 đáy bằng nhau nên là hình thang cân (đpcm)
Nguồn: Nguyễn Nhật Minh (h.vn)
